
【摘要】
工程地质界面(Geo-interface)是指地层中受自然营力和工程活动共同作用的两种或多种介质之间的接触面,以及对三相介质迁移、物态变化和岩土稳定性起控制作用的转换面(朱鸿鹄,2023)。由于自然因素和人类活动的共同作用,工程地质界面在地质灾害的形成、传播和诱发过程中发挥着至关重要的作用。在过去的30年中,物质点法(Material Point Method, MPM)作为一种用于解决大变形问题和模拟土-水-结构相互作用的数值方法,已成为分析工程地质界面演化的重要工具。本文系统综述了工程地质界面的基本概念、分类及其主要特征,并全面概述了近年来利用物质点法模拟工程地质界面的最新进展。同时,简要介绍了物质点法在岩土工程应用中用于模拟不同类型工程地质界面的多种建模方法,并指出了其现有局限性及未来研究方向。本文旨在促进物质点法在复杂工程地质界面模拟中的创新应用,为岩土工程研究者提供参考和借鉴。
【1 研究背景】
研究问题这篇文章要解决的问题是如何利用物质点法(Material Point Method, MPM)进行地质界面建模。地质界面是指地质层之间以及调节三相物质迁移、物理状态变化以及岩土体变形和稳定性的过渡区。研究难点该问题的研究难点包括:准确模拟地质界面的复杂动态特性、处理大变形问题、以及多相相互作用和热-水-力-机械因素的耦合。相关工作过去三十年中,MPM因其在解决大变形问题和模拟土-水-结构相互作用方面的优势,成为地质界面行为分析的理想工具。已有研究探讨了各种数值方法在地质界面建模中的应用,如有限元法(FEM)、离散元法(DEM)等,但它们在处理大变形问题时存在局限性。
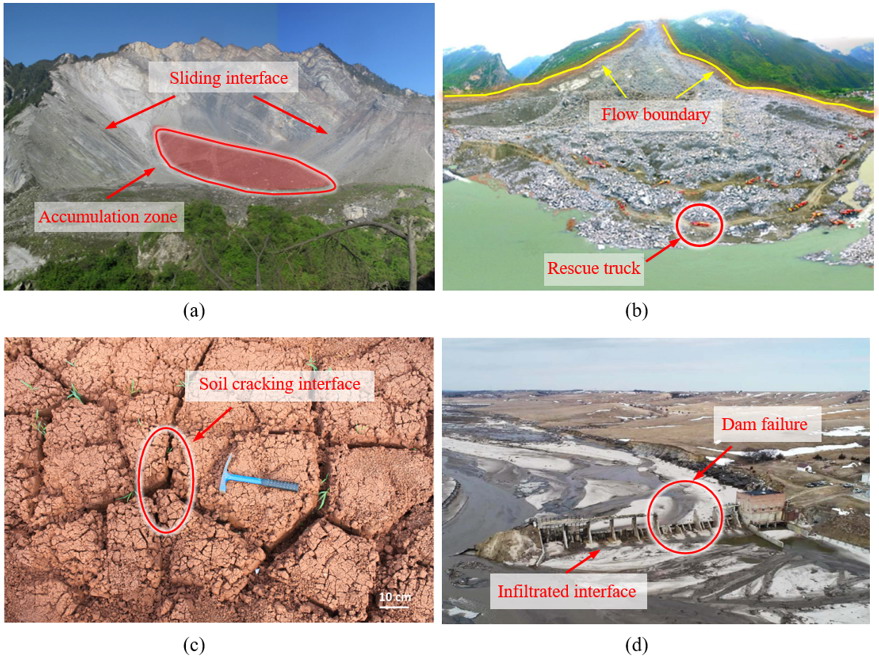
图1. 典型工程地质界面:(a) 大光包滑坡的裸露滑动面;(b) 新磨滑坡的救援现场;(c) 土体龟裂;(d) 大坝溃堤事件
【2 地质界面的数值建模】
2.1 地质界面的分类
材料界面:指地质介质之间的接触表面,如岩石与土壤、土壤与混凝土等。
状态界面:指地质介质中涉及水分、应力或温度等状态参数的突变界面。
运动界面:指地质介质内部或与结构物之间发生的宏观变形和破坏界面。
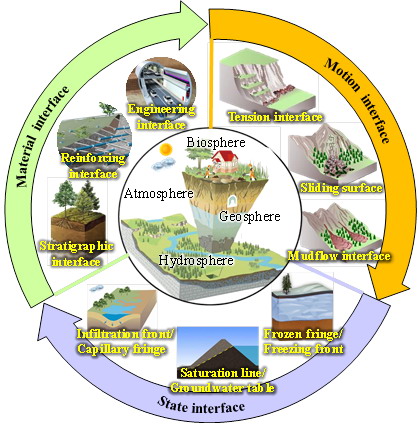
图2. 工程地质界面分类示意图
2.2 数值建模方法的比较
有限元法(FEM):适用于模拟地质界面的应力和变形变化,但在大变形情况下容易因网格畸变导致模拟失败。
欧拉-拉格朗日耦合方法(CEL):适用于处理大变形问题,但数值精度受欧拉网格粗糙度影响。
光滑粒子流体动力学(SPH):适用于模拟流体-固体相互作用,但需要特殊的边界方法和计算效率较低。
颗粒有限元法(PFEM):适用于处理大变形问题和流体-固体耦合,但需要特殊的接触方法。
MPM:适用于模拟复杂地质界面的大变形问题,能够提供多场数据,包括位移、速度和应力信息。
【3 物质点法】
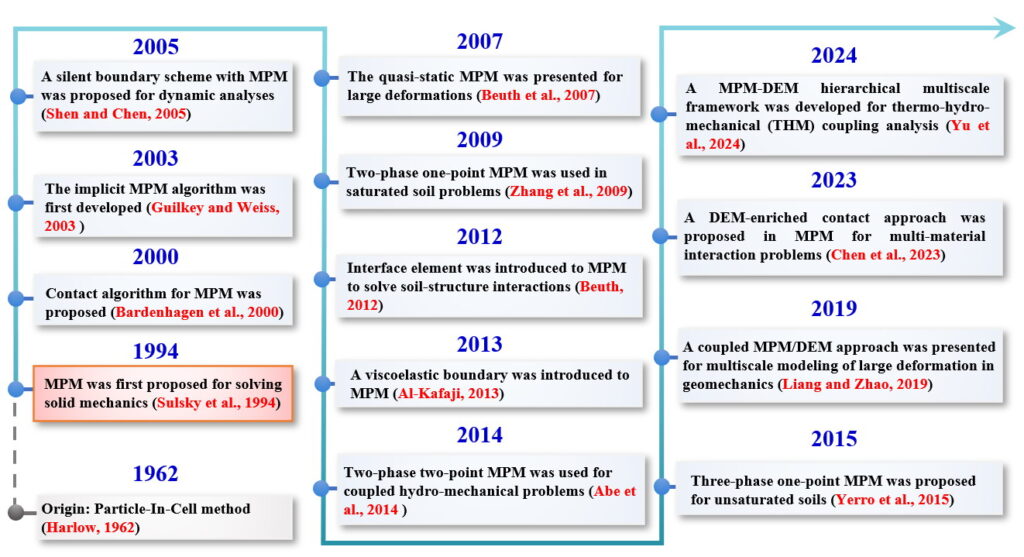
图3. 物质点法发展简史
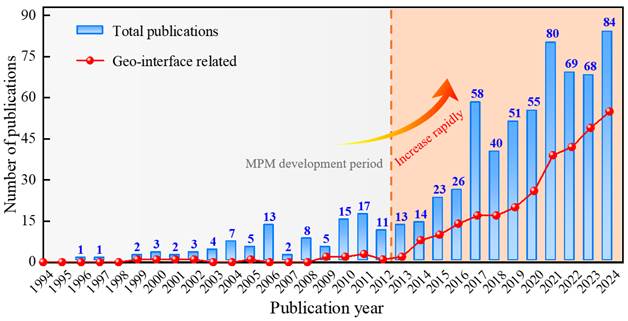
图4. 物质点法相关论文的发文量统计

图5 物质点法(MPM)计算流程示意图
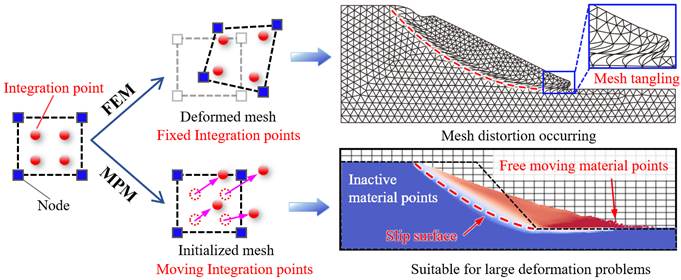
图6. 有限元法与物质点法的工程地质界面模拟结果对比
【4 物质界面的建模】
接触算法:在MPM中,接触算法常用于模拟材料界面。例如,摩擦接触算法广泛应用于土-结构相互作用中。初始预测节点速度在拉格朗日阶段进行,然后使用摩擦接触算法计算修正后的节点速度和加速度。这些更新的节点加速度用于计算MPs的速度,进一步更新其位置、应变和应力。
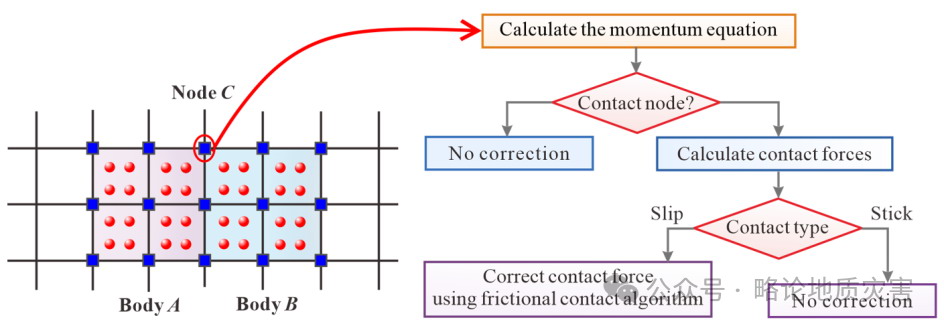
图7 材料点方法(MPM)中的摩擦接触算法原理
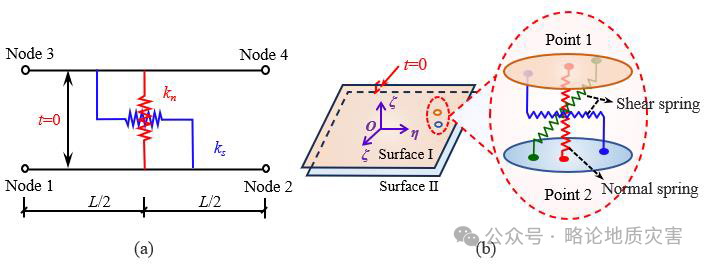
图8 Goodman等(1968)提出的零厚度单元模型
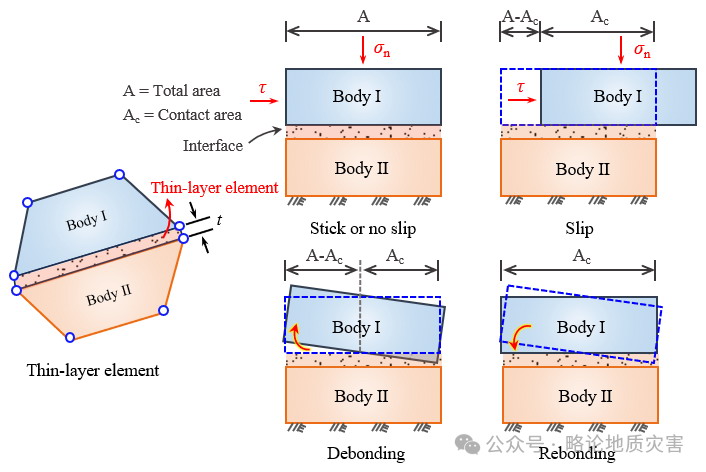
图9 Desai等(1984)提出的薄层单元构型
【5 状态界面的建模】
状态界面指的是涉及土体中水分、应力或温度的状态参数发生突变(Zhu, 2023)的界面。许多研究表明,降雨渗透、地下水位波动和孔隙压力等因素是滑坡(安德森与安德森,2010;刘等人,2019;耶罗等人,2019)、堤防溃决(扎巴拉和阿隆索,2011)以及盾构隧道中的水土涌出(Xie et al., 2022)的主要原因。由于与已得到充分研究的有限元法(FEM)在算法上的相似性,多尺度方法(MPM)在大变形分析中捕捉水-机行为非常有效,特别是使用适当的土壤本构模型时。目前,MPM包括两相单点、两相双点和三相单点法等用于土-水耦合的公式。各种MPM数值方法的细节在图10中进行了说明,并在以下小节中进一步阐述。
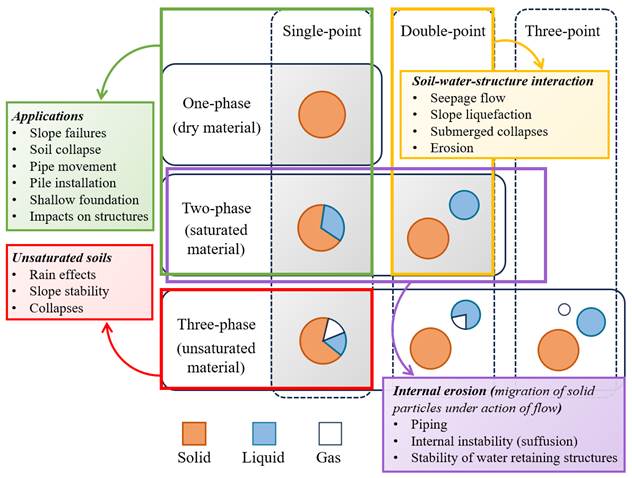
图10. 不同类型物质点法的示意图
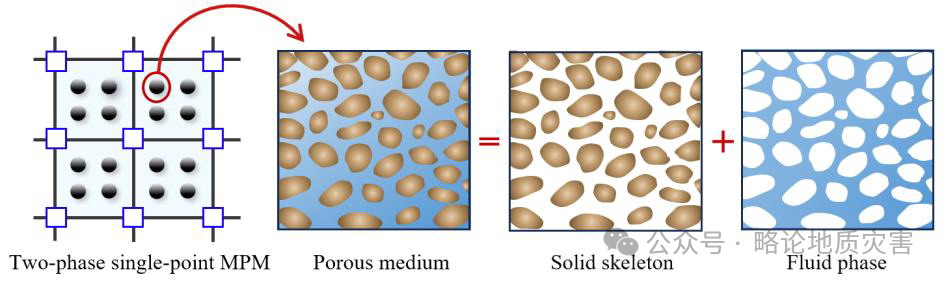
图11 两相单点耦合算法框架
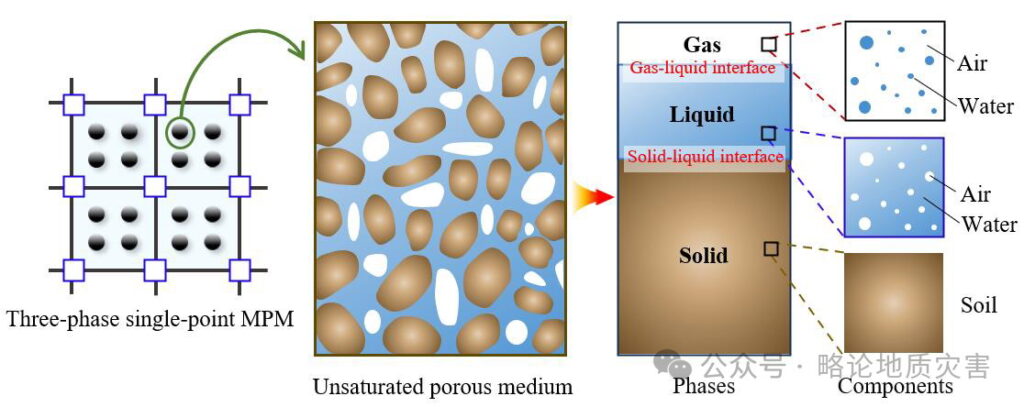
图12 三相单点耦合数值模型

图13 两相双点耦合计算策略
【6 运动界面的建模】
运动界面是指岩石和土体内部或土壤与相邻结构之间的界面上发生的宏观变形和破坏(朱,2023年)。这些界面通常表现为剪切带或滑移面。如前所述,多孔介质中的粒子可以穿过背景网格。因此,在计算映射函数之前,跟踪每个时间步骤的粒子至关重要,以确保准确性(比什等人,2021年;冯和徐,2021年;鲍姆加滕和卡姆林,2023年)。如图14所示,在模拟诸如打桩和浅基础问题等穿透问题时,保持计算精度是必不可少的。在土壤-结构界面附近进行网格细化已被证明是有效的,因为该处解的变化可能迅速发生(陈等人,2019年;王等人,2021b年)。
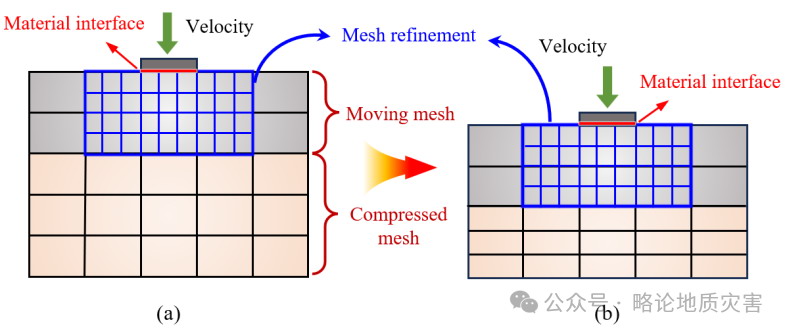
图14 移动网格法的实现机制
【7 实例分析】
7.1边坡失稳和滑坡分析
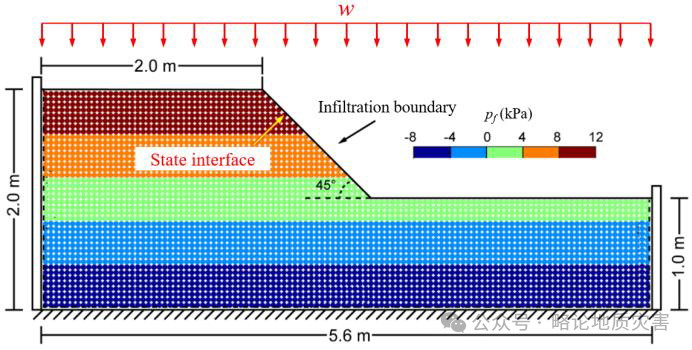
图15 降雨导致滑坡的物质点法模型
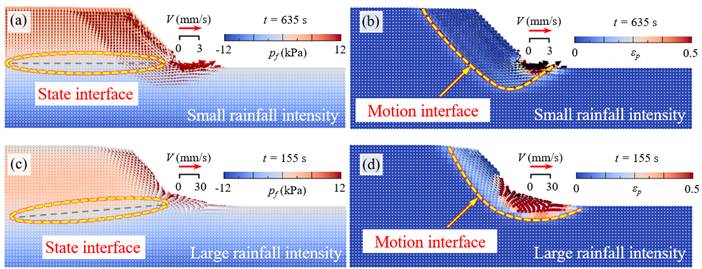
图16. 滑坡形态的物质点法模拟过程
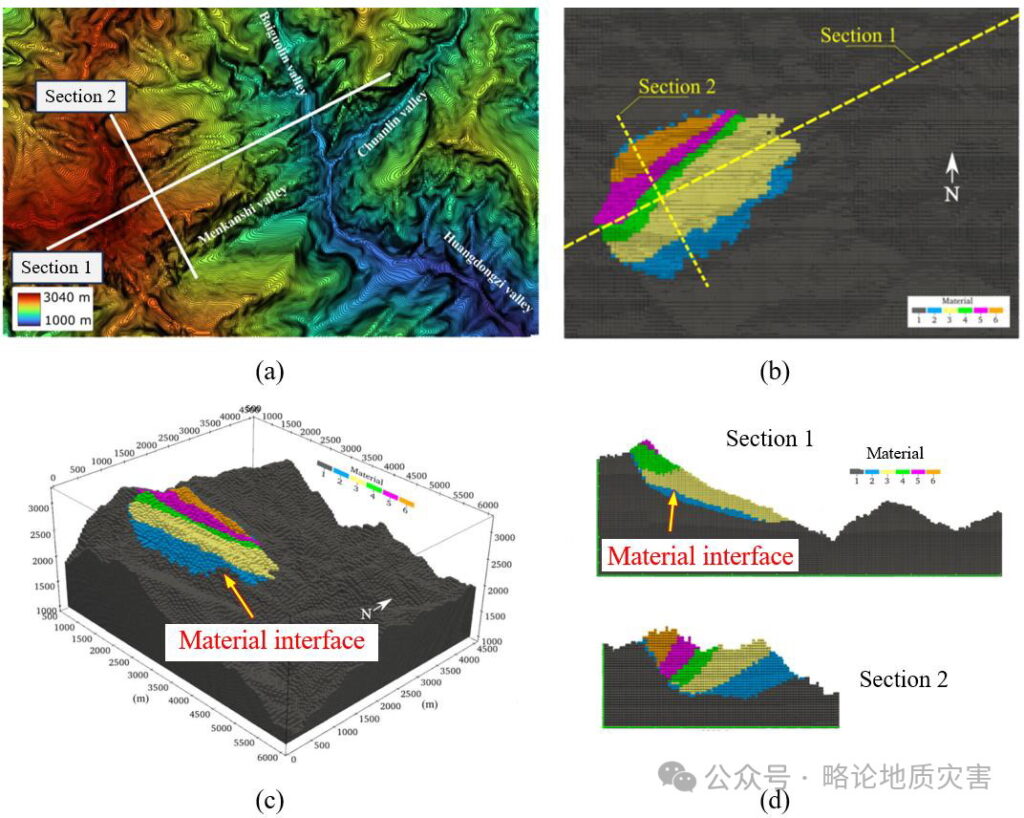
图17.滑坡区域三维地形数据重构
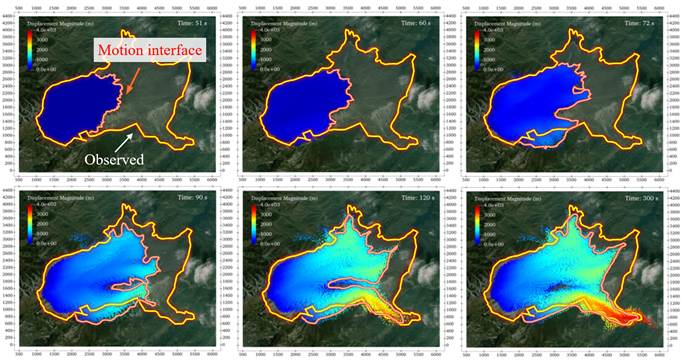
图18. 滑坡运动界面的动态扩展过程
7.2 土-结构相互作用
MPM模拟埋地管道的抬升破坏,结果显示剪切带的形成和转变主要受土壤楔形尺寸、剪切阻力和流动机制的影响。模拟海底滑坡对固定海底管道的影响时,发现冲击系数能够量化滑动碎片对管道施加的应力。
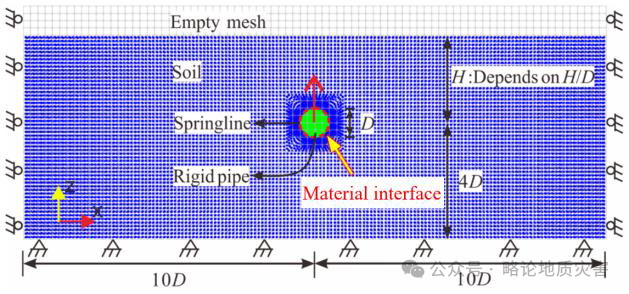
图19 材料点方法(MPM)模型的几何特征与初始材料点分布
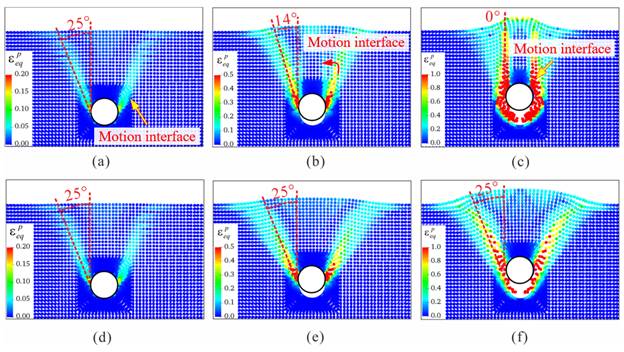
图20. 埋地管道隆升过程中剪切带的演化过程
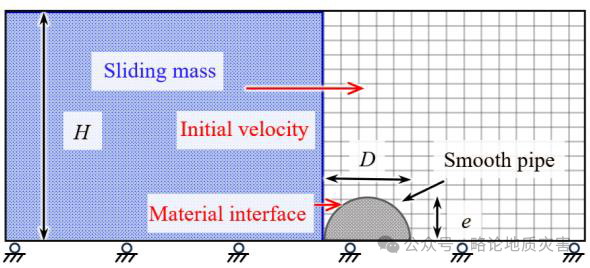
图21 海底滑坡对固定管道的冲击作用数值模拟
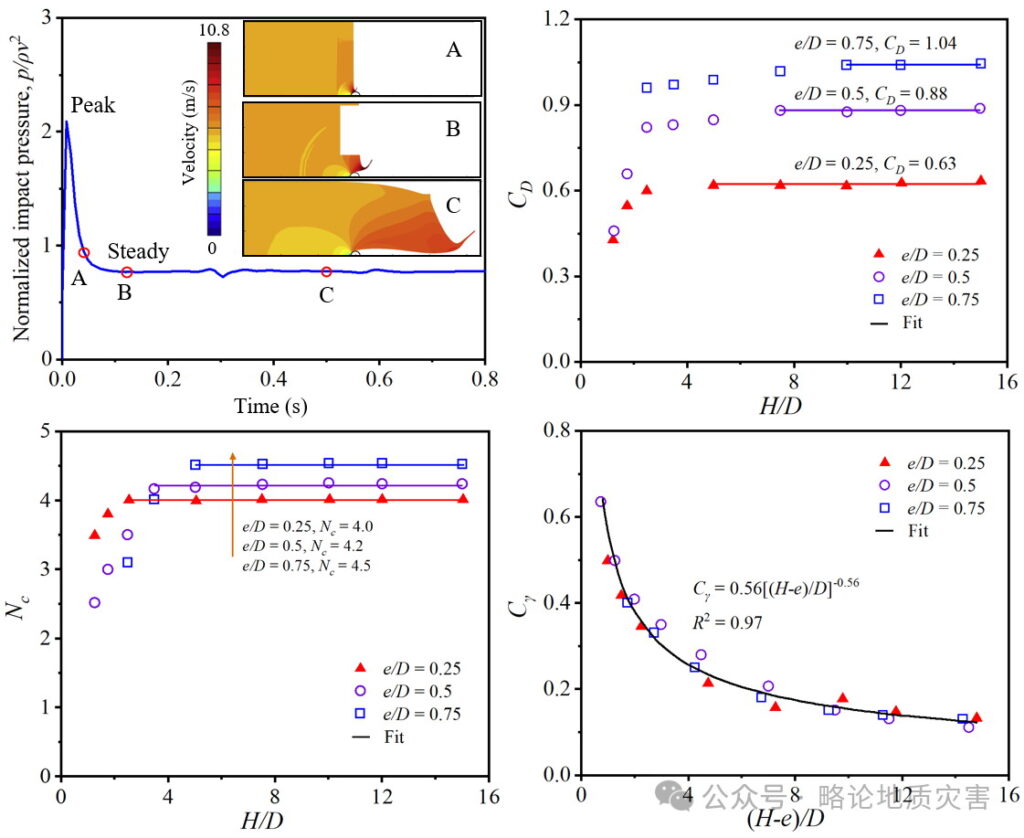
图22 冲击力的回归分析结果
7.3人类活动引起的地质灾害
MPM模拟隧道内的水-土涌出时,发现运动界面的扩展和稳定化与孔隙水压力的变化密切相关。通过监测和分析这些界面,可以采取有效的措施减轻地质灾害的风险。 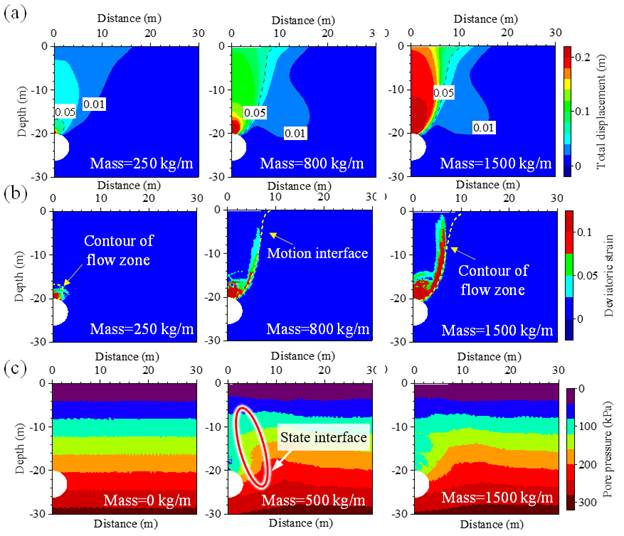
图24. 隧道涌水过程中工程地质界面演化
【8 当前局限性和研究展望】
8.1 局限性
尽管物质点法在工程地质界面模拟方面取得了显著进展,但仍需解决若干挑战,以进一步提高其模拟效果。深入理解这些局限性对于增强物质点法的预测能力及其在工程地质界面模拟中的实际应用具有重要意义。
(1) 在模拟物质界面时,物质点法处理土-结构相互作用问题时采用了相对简化的方式,主要依赖摩擦接触算法。然而,该方法可能无法准确捕捉具有不同材料属性的复杂工程地质界面行为,从而限制了模拟结果的准确性。此外,实际地层结构中裂隙和节理等物质界面的模拟需要极小的网格单元,而网格尺寸的巨大差异会带来显著挑战。
(2) 状态界面通常涉及固相、液相和气相之间的相互作用,因此需要耦合方法来处理复杂的流固耦合问题。物质点法主要基于达西定律描述多孔介质中的液相运动,但该假设在高速流动条件下可能不再适用。当前的物质点模型还缺乏模拟状态界面热传递效应,其在核废料处理或滑坡运动中的研究非常重要。此外,现有模型通常忽略非饱和土中的气体迁移过程,这会显著改变工程地质界面的水力特性。忽视这些因素可能导致模拟结果不够准确。
(3) 为了实现运动界面的高精度模拟,选择合适的土体本构模型至关重要。然而,当前物质点法中常用的模型(如Moh-Croulomb和Drucker-Prager模型)过于理想化,难以描述非线性应力-应变关系并捕捉运动界面的复杂演变。这种局限性降低了模拟精度,尤其是在涉及类固体和类流体行为转换的过渡阶段。此外,应变率、应变硬化/软化以及各向异性等因素对运动界面的演变具有显著影响。工程地质界面处的复杂相互作用(如摩擦滑动等)需要能够处理大位移和偏转的接触算法,现有方法在实现这些功能时仍存在技术挑战。
8.2 研究趋势
为了克服上述讨论的物质点法在模拟工程地质界面方面的局限性,未来的研究应着重于提升物质点法在复杂工程地质界面问题中的适用性,具体建议如下:
(1) 将物质点法与其他数值技术(如有限元法(FEM)、离散元法(DEM)、光滑粒子流体动力学(SPH)、计算流体力学(CFD)、近场动力学(PD)、分子动力学(MD)等相结合,具有广阔的前景。这些混合方法是当前研究的热点领域。通过整合每种技术的优势,这种方法能够推动地质界面的多尺度和多物理场仿真,从而显著提升对工程地质界面演变规律的理解。
(2) 在物质点法中引入考虑各向异性、非线性和时间依赖性的先进本构模型。这些模型能够更准确地捕捉大变形过程中运动界面的演变。此外,将有限元法的界面单元和结构单元嵌入到物质点法中,对于克服接触算法的局限性具有重要意义。这对于模拟土与结构(如桩、锚、土工格栅)之间的物质界面行为具有重要意义。
(3) 将气相作为自由粒子进行模拟,例如土体中的浸润面、垃圾填埋气体迁移以及水位快速下降期间大坝地基的空气流动等。此外,人工智能(AI)技术的快速发展促使许多研究人员将AI与数值模拟方法相结合,以研究岩土工程问题。这种技术能够增强物质点法的预测能力,并有助于识别大型数据集中的失效模式,从而提高物质点法模拟的准确性和可靠性。
【9 结论】
工程地质界面及其相互作用机制在诱发各类地质灾害中发挥着至关重要的作用。模拟这些界面是地质灾害减灾与预防领域的关键科学问题之一。本文旨在全面概述工程地质界面的基本概念、分类及其主要特征,并深入探讨物质点法的基本原理、框架、局限性及未来研究方向。此外,本文还列举了物质点法在工程地质界面分析中的若干应用案例。本综述的主要结论如下:
(1) 物质点法在模拟工程地质界面行为方面展现出巨大潜力,这主要得益于其在大变形模拟中的显著优势。通过模拟不同类型的地质界面(包括物质界面、状态界面和运动界面),物质点法已被证明能够有效模拟土-结构相互作用以及地质灾害(如滑坡和地裂缝)。这使其成为预测地质灾害、加强风险评估与管理的强大模拟手段。
(2) 尽管物质点法在模拟工程地质界面行为方面取得了显著进展,但它仍面临仿真精度、计算效率及多物理场耦合相关的问题。当前模型在处理复杂边界条件、非线性材料变形及长时间尺度问题时存在局限性。为应对这些挑战,未来研究应聚焦于引入先进的本构模型、开发更高效的数值算法以及增强多物理场耦合能力,从而优化物质点法的性能。
(3) 随着数值技术的不断发展,将物质点法与其他数值方法(如有限元法、离散元法等)相结合,可以显著提升工程地质界面模拟的准确性和效率。此外,结合人工智能(AI)技术,能够优化模拟参数的选择和结果分析,从而显著提高工程地质界面模拟的精准度。
Xie, T.C., Zhu, H.-H.*, Dong, Y.K., Zhou, M.L., Wang, B., Zhang, W., Zhao, J.D. (2025). Geo-interface modeling with material point method: A review. Journal of Rock Mechanics and Geotechnical Engineering, 17(6), 3950-3972. DOI: 10.1016/j.jrmge.2025.04.001
Abstract: Geo-interfaces refer to the contact surfaces between multiple media within geological strata, as well as the transition zones that regulate the migration of three-phase matter, changes in physical states, and the deformation and stability of rock and soil masses. Owing to the combined effects of natural factors and human activities, geo-interfaces play crucial roles in the emergence, propagation, and triggering of geological disasters. Over the past three decades, the material point method (MPM) has emerged as a preferred approach for addressing large deformation problems and simulating soil-water-structure interactions, making it an ideal tool for analyzing geo-interface behaviors. In this review, we offer a systematic summary of the basic concepts, classifications, and main characteristics of the geo-interface, and provide a comprehensive overview of recent advances and developments in simulating geo-interface using the MPM. We further present a brief description of various MPMs for modeling different types of geo-interfaces in geotechnical engineering applications and highlight the existing limitations and future research directions. This study aims to facilitate innovative applications of the MPM in modeling complex geo-interface problems, providing a reference for geotechnical practitioners and researchers.
Keywords: Geo-interface; Material point method (MPM); Interaction mechanism; Large deformation; Numerical simulation
References
Abe, K., Konagai, K., 2016. Numerical simulation for runout process of debris flow using depth-averaged material point method. Soils Found. 56(5), 869-888.
Abe, K., Soga, K., Bandara, S., 2014. Material point method for coupled hydromechanical problems. J. Geotech. Geoenviron. Eng. 140(3), 04013033.
Acosta, J.G., Vardon, P.J., Hicks, M.A., 2021a. Study of landslides and soil-structure interaction problems using the implicit material point method. Eng. Geol. 285, 106043.
Acosta, J.L.G., Vardon, P.J., Hicks, M.A., 2021b. Development of an implicit contact technique for the material point method. Comput. Geotech. 130, 103859.
Al-Kafaji, K.I., 2013. Formulation of a dynamic material point method (MPM) for geomechanical problems. PhD thesis. Univ. of Stuttgart, Germany.
Alsardi, A., Yerro, A., 2023. Coseismic site response and slope instability using periodic boundary conditions in the material point method. J. Rock Mech. Geotech. Eng. 15(3), 641-658.
Alvarado, M., Pinyol, N.M., Alonso, E.E., 2019. Landslide motion assessment including rate effects and thermal interactions: Revisiting the Canelles landslide. Can. Geotech. J. 56(9), 1338-1350.
Andersen, S., Andersen, L., 2010. Modelling of landslides with the material-point method. Comput. Geosci. 14, 137-147.
Anura3D, 2020. Anura3D MPM software v_2020. www.anura3d.com.
Bandara, S., Ferrari, A., Laloui, L., 2016. Modelling landslides in unsaturated slopes subjected to rainfall infiltration using material point method. Int. J. Numer. Anal. Methods Geomech. 40(9), 1358-1380.
Bandara, S., Soga, K., 2015. Coupling of soil deformation and pore fluid flow using material point method. Comput. Geotech. 63, 199-214.
Bardenhagen, S.G., 2001. An improved contact algorithm for the material point method and application to stress propagation in granular material. Comput. Model. Eng. Sci. 2(4), 509.
Bardenhagen, S.G., Brackbill, J.U., Sulsky, D., 2000. The material-point method for granular materials. Comput. Methods Appl. Mech. Eng. 187(3-4), 529-541.
Bardenhagen, S.G., Kober, E.M., 2004. The generalized interpolation material point method. Comput. Model. Eng. Sci. 5, 477-496.
Baumgarten, A.S., Kamrin, K., 2023. Analysis and mitigation of spatial integration errors for the material point method. Int. J. Numer. Methods Eng. 1-49.
Beuth, L., 2012. Formulation and application of a quasi-static material point method. PhD thesis. Stuttgart University, Germany.
Beuth, L., Benz, T., Vermeer, P.A., Coetzee, C.J., Bonnier, P., van den Berg, P., 2007. Formulation and validation of a quasi-static material point method. In: 10th International Symposium in Numerical Methods in GeoMechanics. Rhodes, Greece, 189–195.
Beuth, L., Więckowski, Z., Vermeer, P.A., 2011. Solution of quasi‐static large‐strain problems by the material point method. Int. J. Numer. Anal. Methods Geomech. 35(13), 1451-1465.
Bhandari, T., Hamad, F., Moormann, C., Sharma, K.G., Westrich, B., 2016. Numerical modelling of seismic slope failure using MPM. Comput. Geotech. 75, 126-134.
Bishop, A. W., 1955. The use of the slip circle in the stability analysis of earth slopes. Géotechnique 5(1), 7-17.
Bisht, V., Salgado, R., Prezzi, M., 2021. Simulating penetration problems in incompressible materials using the material point method. Comput. Geotech. 133, 103593.
Bojanowski, C., 2014. Numerical modeling of large deformations in soil structure interaction problems using FE, EFG, SPH, and MM-ALE formulations. Arch. Appl. Mech. 84, 743-755.
Budhu, M., 2008. Mechanics of earth fissures using the Mohr-Coulomb failure criterion. Environ. Eng. Geosci. 14(4), 281–295.
Ceccato, F., Beuth, L., Simonini, P., 2016. Analysis of piezocone penetration under different drainage conditions with the two-phase material point method. J. Geotech. Geoenviron. Eng. 142, 04016066.
Ceccato, F., Bisson, A., Cola, S., 2020. Large displacement numerical study of 3D plate anchors. Eur. J. Environ. Civ. Eng. 24, 520-538.
Ceccato, F., Redaelli, I., di Prisco, C., Simonini, P., 2018a. Impact forces of granular flows on rigid structures: Comparison between discontinuous (DEM) and continuous (MPM) numerical approaches. Comput. Geotech. 103, 201-217.
Ceccato, F., Simonini, P., 2017. Numerical study of partially drained penetration and pore pressure dissipation in piezocone test. Acta Geotech. 12, 195-209.
Ceccato, F., Yerro, A., Di Carluccio, G., 2024. Simulating landslides with the material point method: Best practices, potentialities, and challenges. Eng. Geol. 107614.
Ceccato, F., Yerro, A., Martinelli, M., 2018b. Modelling soil-water interaction with the material point method. Evaluation of single-point and double-point formulations. CRC Press, 351.
Chaloulos, Y.K., Bouckovalas, G.D., Karamitros, D.K., 2017. Trench effects on lateral py relations for pipelines embedded in stiff soils and rocks. Comput. Geotech. 83, 52-63.
Chaloulos, Y.K., Bouckovalas, G.D., Zervos, S.D., Zampas, A.L., 2015. Lateral soil–pipeline interaction in sand backfill: Effect of trench dimensions. Comput. Geotech. 69, 442-451.
Charlton, T., Coombs, W., Augarde, C., 2017. IGIMP: an implicit generalised interpolation material point method for large deformations. Comput. Struct. 190,108–125.
Chen, H., Zhao, S., Zhao, J., Zhou, X., 2023. DEM-enriched contact approach for material point method. Comput. Methods Appl. Mech. Eng. 404, 115814.
Chen, J.S., Hillman, M., Chi, S.W., 2017. Meshfree methods: progress made after 20 years. J. Eng. Mech. 143, 04017001.
Chen, X., Li, D., Tang, X., Liu, Y., 2021. A three-dimensional large-deformation random finite-element study of landslide runout considering spatially varying soil. Landslides 18(9), 3149-3162.
Chen, Y., Zhao, W., Han, J., Jia, P., 2019. A CEL study of bearing capacity and failure mechanism of strip footing resting on c-φ soils. Comput. Geotech. 111, 126-136.
Cheng, W.C., Li, G., Liu, N., Xu, J., Horpibulsuk, S., 2020. Recent massive incidents for subway construction in soft alluvial deposits of Taiwan: A review. Tunn. Undergr. Space Technol. 96, 103178.
Cheon, Y.J., Kim, H.G., 2018. An efficient contact algorithm for the interaction of material particles with finite elements. Comput. Methods Appl. Mech. Eng. 335, 631–659.
Chu L.M., Yin, J.H., 2005. Comparison of interface shear strength of soil nails measured by both direct shear box tests and pullout tests. J. Geotech. Geoenviron. Eng.131(9), 1097-1107.
Coetzee, C.J., Vermeer, P.A., Basson, A.H., 2005. The modelling of anchors using the material point method. Int. J. Numer. Anal. Methods Geomech. 29, 879-895.
Conte, E., Pugliese, L., Troncone, A., 2019. Post-failure stage simulation of a landslide using the material point method. Eng. Geol. 253, 149-159.
Conte, E., Pugliese, L., Troncone, A., 2020. Post-failure analysis of the Maierato landslide using the material point method. Eng. Geol. 277, 105788.
Cuomo, S., Di Perna, A., Martinelli, M., 2021a. MPM Modelling of Buildings Impacted by Landslides. In: Workshop on World Landslide Forum. Springer, 245-266.
Cuomo, S., Di Perna, A., Martinelli, M., 2021b. Material point method (MPM) hydro-mechanical modelling of flows impacting rigid walls. Can. Geotech. J. 58(11), 1730-1743.
Cuomo, S., Di Perna, A., Martinelli, M., 2021c. Modelling the spatio-temporal evolution of a rainfall-induced retrogressive landslide in an unsaturated slope. Eng. Geol. 294, 106371.
Cuomo, S., Di Perna, A., Martinelli, M., 2022. Analytical and numerical models of debris flow impact. Eng. Geol. 308, 106818.
Cuomo, S., Di Perna, A., Moscariello, A., Martinelli, M., 2023. Possible remediation of impact-loading debris avalanches via fine long rooted grass: an experimental and material point method (MPM) analysis. Landslides 21(4), 679-696.
Cuomo, S., Di Perna, A., Savino, S., Frigo, B., Martinelli, M., 2024. Reinforced embankments impacted by landslides: Analytical and numerical modelling. Geosynthetics: Leading the Way to a Resilient Planet 915-921.
Day, R.A., Potts, D.M., 1994. Zero thickness interface elements—numerical stability and application. Int. J. Numer. Anal. Methods Geomech. 18, 689-708.
de Vaucorbeil, A., Nguyen, V.P., Sinaie, S., Wu, J.Y., 2020. Material point method after 25 years: Theory, implementation, and applications. Adv. Appl. Mech. 53, 185-398.
DeJong, J.T., White, D.J., Randolph, M.F., 2006. Microscale observation and modeling of soil-structure interface behavior using particle image velocimetry. Soils Found. 46, 15-28.
Deng, L.C., Zhang, W., Deng, L., Shi, Y. H., Zi, J.J., He, X., Zhu, H.H., 2024. Forecasting and early warning of shield tunnelling-induced ground collapse in rock-soil interface mixed ground using multivariate data fusion and Catastrophe Theory. Eng. Geol. 335, 107548.
Desai, C.S., Zaman, M.M., Lightner, J.G., Siriwardane, H.J., 1984. Thin‐layer element for interfaces and joints. Int. J. Numer. Anal. Methods Geomech. 8, 19-43.
Dhadse, G.D., Ramtekkar, G., Bhatt, G., 2023. A succinct review on soil structure interface thickness. Arch. Comput. Methods Eng. 1-8.
Dhadse, G.D., Ramtekkar, G.D., Bhatt, G., 2021. Finite element modeling of soil structure interaction system with interface: A review. Arch. Comput. Methods Eng. 28, 3415-3432.
Dong, Y., 2020. Reseeding of particles in the material point method for soil–structure interactions. Comput. Geotech. 127, 103716.
Dong, Y., Wang, D., Cui, L., 2020a. Assessment of depth-averaged method in analysing runout of submarine landslide. Landslides 17, 543-555.
Dong, Y., Wang, D., Randolph, M.F., 2015. A GPU parallel computing strategy for the material point method. Comput. Geotech. 66, 31-38.
Dong, Y., Wang, D., Randolph, M.F., 2017a. Investigation of impact forces on pipeline by submarine landslide using material point method. Ocean Eng. 146, 21-28.
Dong, Y., Wang, D., Randolph, M.F., 2017b. Runout of submarine landslide simulated with material point method. J. Hydrodyn. 29(3), 438-444.
Dong, Y., Wang, D., Randolph, M.F., 2020b. Quantification of impact forces on fixed mudmats from submarine landslides using the material point method. Appl. Ocean Res. 102, 102227.
Du, W., Sheng, Q., Fu, X., Chen, J., Wei, P., Zhou, Y., 2023. Post-failure analysis of landslide blocking river using the two-phase double-point material point method: a case of western Hubei, China. Bull. Eng. Geol. Environ. 82(3), 98.
Du, W., Sheng, Q., Fu, X., Chen, J., Zhou, Y., 2021. Extensions of the two-phase double-point material point method to simulate the landslide-induced surge process. Eng. Anal. Bound. Elem. 133, 362-375.
Duncan, J.M., 1996. State of the art: Limit equilibrium and finite element analysis of slopes. J. Geotech. Eng. 122 (7), 577–596.
Ettema, R., Baker, M.E., Teal, M., Trojanowski, J., 2024. Ice-Run Destruction of Spencer Dam on Nebraska’s Niobrara River. In CGU HS Committee on River Ice Processes and the Environment, 21st Workshop on the Hydraulics of Ice-Covered Rivers, Saskatoon, Saskatchewan, Canada.
Fang, K., Dong, A., Tang, H., An, P., Wang, Q., Jia, S., Zhang, B., 2024. Development of an easy-assembly and low-cost multismartphone photogrammetric monitoring system for rock slope hazards. Int. J. Rock Mech. Min. Sci. 174, 105655.
Feng, K., Huang, D., Wang, G., 2021. Two-layer material point method for modeling soil–water interaction in unsaturated soils and rainfall-induced slope failure. Acta Geotech. 16(8), 2529-2551.
Feng, Z.K., Xu, W.J., 2021. GPU material point method (MPM) and its application on slope stability analysis. Bull. Eng. Geol. Environ. 80(7), 5437-5449.
Fern, E.J., de Lange, D.A., Zwanenburg, C., Teunissen, J.A.M., Rohe, A., Soga, K., 2017. Experimental and numerical investigations of dyke failures involving soft materials. Eng. Geol. 219, 130-139.
Fern, J., Rohe, A., Soga, K., Alonso, E., 2019. The Material Point Method for Geotechnical Engineering: A Practical Guide. CRC Press.
Fernández, F., do Amaral Vargas, E., Quadros Velloso, R., 2020. A 3D discretization procedure for the material point method (MPM). Comput. Particle Mech. 7, 725–733.
Fernández, F., Vargas Jr, E., Muller, A.L., Sousa, R.L., Sousa, L.R., 2023. Material point method modeling in 3D of the failure and run-out processes of the Daguangbao landslide. Acta Geotech. 1-20.
Frost, J.D., DeJong, J.T., Recalde, M., 2002. Shear failure behavior of granular–continuum interfaces. Eng. Fract. Mech. 69(17), 2029-2048.
Frost, J.D., Han, J. 1999, Behavior of interfaces between fiber reinforced polymers and sands. J. Geotech. Geoenviron. Eng. 125(8), 633–640.
Frost, J.D., Hebeler, G.L., Evans, T.M., DeJong, J.T., 2004. Interface behavior of granular soils. In: Proc. earth and space conference, Houston, TX, 65-72.
Fu, S., Yang, Z.X., Guo, N., Jardine, R.J., 2024. Material point method simulations of displacement pile and CPT penetration in sand considering the effects of grain breakage. Comput. Geotech. 166, 105945.
Galavi, V., Martinelli, M., 2024. MPM Simulation of the Installation of an Impact-Driven Pile in Dry Sand and Subsequent Axial Bearing Capacity. J. Geotech. Geoenviron. Eng. 150(4), 04024019.
Gao, L., Liao, D., Mo, P.Q., 2023. Modeling footing resting on anisotropic sand using material point method. J. Rock Mech. Geotech. Eng. 15(12), 3271-3290.
Gazetas, G., Tassoulas, J., 1987. Horizontal stiffness of arbitrarily shaped embedded foundations. J. Geotech. Eng. 113(5), 440-457.
Girardi, V., Ceccato, F., Rohe, A., Simonini, P., Gabrieli, F., 2023. Failure of levees induced by toe uplift: Investigation of post-failure behavior using material point method. J. Rock Mech. Geotech. Eng. 15(4), 970-983.
Girardi, V., Yerro, A., Ceccato, F., Simonini, P., 2021. Modelling deformations in water retention structures with unsaturated material point method. Proc. Inst. Civ. Eng. Geotech. Eng. 174(5), 577-592.
Given, J., Liang, Y., Zeng, Z., Zhang, X., Soga, K., 2024. The virtual stress boundary method to impose nonconforming Neumann boundary conditions in the material point method. Comp. Part. Mech. 1-25.
Goodman, R.E., Shi, G., 1985. Block theory and its application to rock engineering. Prentice-Hall Inc., New Jersey, USA.
Goodman, R.E., Taylor, R.L., Brekke, T.L., 1968. A model for the mechanics of jointed rock. J. Soil Mech. Found. Div. 94(3), 637-659.
Guilkey, J.E., Weiss, J.A., 2003. Implicit time integration for the material point method: Quantitative and algorithmic comparisons with the finite element method. Int. J. Numer. Meth. Eng. 57(9), 1323-1338.
Harlow, F.H., 1962. The particle-in-cell method for numerical solution of problems in fluid dynamics. Los Alamos National Lab. (LANL), Los Alamos, NM (United States), LADC-5288.
Hashimoto, R., Bodhinanda, C., Soga, K., 2022. A coupled implicit MPM-DDA for soil-structure interaction problems. In: Proc. WCCM-APCOM 2714.
He, M., e Sousa, L.R., Müller, A., Vargas Jr, E., Sousa, R.L., Oliveira, C.S., Gong, W., 2019. Numerical and safety considerations about the Daguangbao landslide induced by the 2008 Wenchuan earthquake. J. Rock Mech. Geotech. Eng. 11(5), 1019-1035.
Higo, Y., Oka, F., Kimoto, S., Morinaka, Y., Goto, Y., Chen, Z., 2010. A coupled MPM-FDM analysis method for multi-phase elasto-plastic soils. Soils Found. 50(4), 515-532.
Hosseini, M.R., Martek, I., Zavadskas, E.K., Aibinu, A.A., Arashpour, M., Chileshe, N., 2018. Critical evaluation of off-site construction research: A Scientometric analysis. Autom. Constr. 87, 235-247.
Hu, L., Pu, J., 2004. Testing and modeling of soil-structure interface. J. Geotech. Geoenviron. Eng. 130(8), 851-860.
Hu, W., Huang, R., McSaveney, M., Yao, L., Xu, Q., Feng, M., Zhang, X., 2019. Superheated steam, hot CO2 and dynamic recrystallization from frictional heat jointly lubricated a giant landslide: field and experimental evidence. Earth Planet. Sci. Lett. 510, 85-93.
Hu, X., Bürgmann, R., Schulz, W.H., Fielding, E.J., 2020. Four-dimensional surface motions of the Slumgullion landslide and quantification of hydrometeorological forcing. Nat. Commun. 11, 2792.
Huang, B., Liu, J., Fan, J., Ling, D., 2021. Experimental study on uplift mechanisms of pipes buried in sloping medium dense sand. J. Pipeline Syst. Eng. Pract. 12(3), 04021027.
Huang, B., Liu, J., Ling, D., Zhou, Y., 2015. Application of particle image velocimetry (PIV) in the study of uplift mechanisms of pipe buried in medium dense sand. J. Civ. Struct. Health Monit. 5(5), 599-614.
Huang, L., Ma, J., Lei, M., Liu, L., Lin, Y., Zhang, Z., 2020. Soil-water inrush induced shield tunnel lining damage and its stabilization: A case study. Tunn. Undergr. Space Technol. 97, 103290.
Huo, Y.X., Gomaa, S.M., Zayed, T., Meguid, M., 2023. Review of analytical methods for stress and deformation analysis of buried water pipes considering pipe-soil interaction. Undergr. Space 13, 205-227.
Jakob, M., Stein, D., Ulmi, M., 2012. Vulnerability of buildings to debris flow impact. Nat. Hazards 60(2), 241-261.
Jassim, I., Stolle, D., Vermeer, P., 2013. Two‐phase dynamic analysis by material point method. Int. J. Numer. Anal. Methods Geomech. 37(15), 2502-2522.
Jiang, Y., Li, M., Jiang, C., Alonso-Marroquin, F., 2020. A hybrid material-point spheropolygon-element method for solid and granular material interaction. Int. J. Numer. Methods Eng. 121 (14), 3021–3047.
Jiang, Y., Zhao, Y., Choi, C.E., Choo, J., 2022. Hybrid continuum-discrete simulation of granular impact dynamics. Acta Geotech. 17, 5597–5612.
Kalantari, A.R., Johari, A., Zandpour, M., Kalantari, M., 2023. Effect of spatial variability of soil properties and geostatistical conditional simulation on reliability characteristics and critical slip surfaces of soil slopes. Transp. Geotech. 39, 100933.
Kim, D., Kim, T., Kim, Y., Byun, Y.H., Yun, T.S., 2024. A ChatGPT-MATLAB framework for numerical modeling in geotechnical engineering applications. Comput. Geotech. 169, 106237.
King, L., Bouazza, A., Maksimenko, A., Gates, W.P., Dubsky, S., 2019. Measurement of three-dimensional displacement field in piled embankments using synchrotron X-ray tomography. Can. Geotech. J. 56(6), 885-892.
Kiriyama, T., Higo, Y., 2020. Arbitrary particle domain interpolation method and application to problems of geomaterial deformation. Soils Found. 60(6), 1422-1439.
Kirschbaum, D.B., Adler, R., Hong, Y., Hill, S., Lerner-Lam, A., 2010. A global landslide catalog for hazard applications: method, results, and limitations. Nat. Hazards 52(3), 561-575.
Kounlavong, K., Chavda, J. T., Jamsawang, P., Keawsawasvong, S., 2023. Stability analysis of buried pipelines under combined uplift and lateral forces using FELA and ANN. Appl. Ocean Res. 135, 103568.
Le, T.C., Liu, C., Tang, C.S., Zhang, X.Y., Shi, B., 2022. Numerical simulation of desiccation cracking in clayey soil using a multifield coupling discrete-element model. J. Rock Mech. Geotech. Eng. 148(2), 04021183.
Lee, M., Martinelli, M., Shieh, C.L., 2019a. Modelling rainfall-induced landslides with the material point method: the Fei Tsui Road case. Proceedings of the XVII ECSMGE.
Lee, M., Martinelli, M., Shieh, C.L., 2019b. Numerical Analysis of the Shiaolin Landslide using material point method. In 7th International Symposium on Geotechnical Safety and Risk, 11-13.
Lee, M., Martinelli, M., Shieh, C.L., 2021. An investigation of rainfall-induced landslides from the pre-failure stage to the post-failure stage using the material point method. Front. Earth Sci. 9, 764393.
Lenardic, A., Moresi, L., Muhlhaus, H., 2000. The role of mobile belts for the longevity of deep cratonic lithosphere: the crumpled zone model. Geophys. Res. Lett. 27(8), 1235-1238.
Li, J., Wang, B., Pan, P., Chen, H., Wang, D., Chen, P., 2024. Failure analysis of soil-rock mixture slopes using coupled MPM-DEM method. Comput. Geotech. 169, 106226.
Li, S., Zhang, Y., Wu, J., Yu, J., Gong, X., 2021a. Modeling of crack propagation with the quasi-static material point method. Eng. Fract. Mech. 245, 107602.
Li, S., Zhang, Y., Wu, J., Yu, J., Gong, X., 2023a. Numerical modeling of pumping-induced earth fissures using coupled quasi-static material point method. J. Geotech. Geoenviron. Eng. 149(9), 04023065.
Li, W.L., Guo, N., Yang, Z.X., Helfer, T., 2021b. Large-deformation geomechanical problems studied by a shear-transformation-zone model using the material point method. Comput. Geotech. 135, 104153.
Li, X., Fang, Y., Li, M., Jiang, C., 2022a. BFEMP: Interpenetration-free MPM–FEM coupling with barrier contact. Comput. Methods Appl. Mech. Eng. 390, 114350.
Li, X., Wu, Y., He, S., Su, L., 2016. Application of the material point method to simulate the post-failure runout processes of the Wangjiayan landslide. Eng. Geol. 212, 1-9.
Li, X., Yan, Q., Zhao, S., Luo, Y., Wu, Y., Wang, D., 2020. Investigation of influence of baffles on landslide debris mobility by 3D material point method. Landslides 17, 1129-1143.
Li, X., Yao, J., Sun, Y., Wu, Y., 2022. Material point method analysis of fluid–structure interaction in geohazards. Nat. Hazards 114, 3425-3443.
Li, Z., Huang, H., Zhou, M., Zhang, D., 2023b. Failure responses of rock tunnel faces during excavation through the fault-fracture zone. Undergr. Space 10, 166-181.
Lian, Y., Zhang, X., Zhou, X., Ma, Z., 2011. A FEMP method and its application in modeling dynamic response of reinforced concrete subjected to impact loading. Comput. Methods Appl. Mech. Eng. 200(17–20), 1659–1670.
Liang, D., Zhao, X., Soga, K., 2020. Simulation of overtopping and seepage induced dike failure using two-point MPM. Soils Found. 60, 978-988.
Liang, W., Wu, H., Zhao, S., Zhou, W., Zhao, J., 2022. Scalable three‐dimensional hybrid continuum‐discrete multiscale modeling of granular media. Int J Numer. Methods Eng. 123, 2872-2893.
Liang, W., Zhao, J., 2019. Multiscale modeling of large deformation in geomechanics. Int. J. Numer. Anal. Methods Geomech. 43 (5), 1080-1114.
Liang, W., Zhao, J., Wu, H., Soga, K., 2023a. Multiscale, multiphysics modeling of saturated granular materials in large deformation. Comput. Methods Appl. Mech. Eng. 405, 115871.
Liang, Y., Given, J., Soga, K., 2023b. The imposition of nonconforming Neumann boundary condition in the material point method without boundary representation. Comput. Methods Appl. Mech. Eng. 404, 115785.
Liao, Z., Ren, M., Tang, C., Zhu, J., 2020. A three-dimensional damage-based contact element model for simulating the interfacial behaviors of rocks and its validation and applications. Geomech Geophys Geo-Energy Geo-Resour. 6(03), 1–21.
Liu, C., Sun, Q., Jin, F., Zhou, G.G., 2017. A fully coupled hydro-mechanical material point method for saturated dense granular materials. Powder Technol. 314, 110-120.
Liu, C., Sun, Q., Zhou, G.G.D., 2018. Coupling of material point method and discrete element method for granular flows impacting simulations. Int. J. Numer. Methods Eng. 115, 172-188.
Liu, K., Wang, Y., Huang, M., Yuan, W.H., 2021. Postfailure analysis of slopes by random generalized interpolation material point method. Int. J. Geomech. 21, 04021015.
Liu, L.L., Zhang, P., Zhang, S.H., Li, J.Z., Huang, L., Cheng, Y.M., Wang, B., 2022. Efficient evaluation of run-out distance of slope failure under excavation. Eng. Geol. 306, 106751.
Liu, X., Wang, Y., 2021. Probabilistic simulation of entire process of rainfall-induced landslides using random finite element and material point methods with hydro-mechanical coupling. Comput. Geotech. 132, 103989.
Liu, X., Wang, Y., Li, D.Q., 2019. Investigation of slope failure mode evolution during large deformation in spatially variable soils by random limit equilibrium and material point methods. Comput. Geotech. 111, 301-312.
Liu, X., Wang, Y., Li, D.Q., 2020. Numerical simulation of the 1995 rainfall-induced Fei Tsui Road landslide in Hong Kong: new insights from hydro-mechanically coupled material point method. Landslides 17, 2755-2775.
Llano-Serna, M.A., Farias, M.M., Pedroso, D.M., 2016. An assessment of the material point method for modelling large scale run-out processes in landslides. Landslides 13, 1057-1066.
Locat, J., Lee, H.J., 2002. Submarine landslides: advances and challenges. Can. Geotech. J. 39 (1), 193-212.
Lu, M., Ceccato, F., Zhou, M., Yerro, A., Zhang, J., 2023. Evaluating the exceedance probability of the runout distance of rainfall-induced landslides using a two-stage FEM-MPM approach. Acta Geotech. 19, 3691–3706.
Luco, J.E., 1998. A simple model for structural control including soil–structure interaction effects. Earthquake Eng. Struct. Dyn. 27(3), 225-242.
Luo, G., Yan, C., Li, X., Jiang, J., Ma, J., 2003. Exploration of water resource and multiple model for water resource development in karst areas with the preferred plane theory. Acta Geologica Sinica‐English Edition, 77(1), 129-135.
Lysmer, J., Kuhlemeyer, R.L., 1969. Finite dynamic model for infinite media. J. Eng. Mech. Div. 95(4), 859-877.
Ma, J., Wang, D., Randolph, M.F., 2014. A new contact algorithm in the material point method for geotechnical simulations. Int. J. Numer. Anal. Meth. Geomech. 38, 1197-1210.
Martinelli, M., 2016. Soil-water interaction with material point method. Double-point formulation.
Martinelli, M., Galavi, V., 2021. Investigation of the Material Point Method in the simulation of Cone Penetration Tests in dry sand. Comput. Geotech. 130, 103923.
Martinelli, M., Galavi, V., 2022. An explicit coupled MPM formulation to simulate penetration problems in soils using quadrilateral elements. Comput. Geotech. 145, 104697.
Martinelli, M., Lee, M., Shieh, C.L., Cuomo, S., 2020. Rainfall boundary condition in a multiphase Material Point Method. In: Workshop on World Landslide Forum. Springer, 303-309.
Martinelli, M., Rohe, A., Soga, K., 2017a. Modeling dike failure using the material point method. Procedia Eng. 175, 341-348.
Martinelli, M., Tehrani, P.H., Galavi, V., 2017b. Analysis of Crater Development Around Damaged Pipelines Using the Material Point Method. Procedia Eng. 175, 204-211.
Mast, C.M., Arduino, P., Miller, G.R., Mackenzie-Helnwein, P., 2014. Avalanche and landslide simulation using the material point method: flow dynamics and force interaction with structures. Comput. Geosci. 18, 817-830.
Monzer, A., Faramarzi, A., Yerro, A., Chapman, D., 2023. MPM Investigation of the fluidization initiation and postfluidization mechanism around a pressurized leaking Pipe. J. Geotech. Geoenviron. Eng. 149, 04023096.
Nakamura, K., Matsumura, S., Mizutani, T., 2021. Particle-to-surface frictional contact algorithm for material point method using weighted least squares. Comput. Geotech. 134, 104069.
Nayroles, B., Touzot, G., Villon, P., 1992. Generalizing the finite element method: Diffuse approximation and diffuse elements. Comput. Mech. 10(5), 307–318.
Nguyen, D.K., Nguyen, T.P., Ngamkhanong, C., Keawsawasvong, S., Nguyen, T.K., 2023. Prediction of uplift resistance of circular anchors in anisotropic clays using MLR, ANN, and MARS. Appl. Ocean Res. 136, 103584.
Nguyen, T.S., Yang, K.H., Wu, Y.K., Teng, F., Chao, W.A., Lee, W.L., 2022. Post-failure process and kinematic behavior of two landslides: Case study and material point analyses. Comput. Geotech. 148, 104797.
Onyelowe, K.C., Fazel Mojtahedi, F., Golaghaei Darzi, A., Kontoni, D.P.N., 2023. Solving large deformation problems in geotechnical and geo-environmental engineering with the smoothed particle hydrodynamics: a state-of-the-art review of constitutive solutions. Environ. Earth Sci. 82(17), 394.
O’Rourke, T.D., 2010. Geohazards and large, geographically distributed systems. Géotechnique 60(7), 505-543.
Pande, G.N., Sharma, K.G., 1979. On joint/interface elements and associated problems of numerical ill‐conditioning. Int. J. Numer. Anal. Methods Geomech. 3(3), 293-300.
Paniagua, P., Andó, E., Silva, M., Emdal, A., Nordal, S., Viggiani, G. 2013. Soil deformation around a penetrating cone in silt. Géotechnique Letters 3(4), 185–191.
Pastor, M., Tayyebi, S.M., Stickle, M.M., Yagüe, N., Manzanal, D., 2021. A depth integrated, coupled, two-phase model for debris flow propagation. Acta Geotech. 2, 1–25.
Pastor, M., Yague, A., Stickle, M.M., Manzanal, D., Mira, P., 2018. A two-phase SPH model for debris flow propagation. Int. J. Numer. Anal. Method Geomech. 42(3), 418–448.
Peng, J., Sun, X., Lu, Q., Meng, L., He, H., Qiao, J., Wang, F., 2020. Characteristics and mechanisms for origin of earth fissures in Fenwei basin, China. Eng. Geol. 266, 105445.
Perna, A., Cuomo, S., Martinelli, M., 2022a. Empirical formulation for debris flow impact and energy release. Geoenviron. Disasters. 9(1), 8.
Perna, A., Cuomo, S., Martinelli, M., 2022b. Impact Forces and Energy of Flow-like Landslides Against Protection Barriers: a New MPM-validated Empirical Formulation. Geoenviron. Disasters.
Phuong, N.T.V., Van Tol, A.F., Elkadi, A.S.K., Rohe, A., 2016. Numerical investigation of pile installation effects in sand using material point method. Comput. Geotech. 73, 58-71.
Qin, J., Mei, G., Xu, N., 2022. Meshfree methods in geohazards prevention: a survey. Arch. Comput. Meth. Eng. 29(5), 3151-3182.
Qiu, G., Henke, S., Grabe, J., 2011. Application of a Coupled Eulerian–Lagrangian approach on geomechanical problems involving large deformations. Comput. Geotech. 38(1), 30-39.
Raymond, S.J., Jones, B., Williams, J.R., 2016. A strategy to couple the material point method (MPM) and smoothed particle hydrodynamics (SPH) computational techniques. Comput. Particle Mech. 5, 49-58.
Reissner, E., 1936. Stationare, axialsymmetrische, durch eine schuttelnde masses erregte schwingungen elastischen halbraumes. Arch. Appl. Mech. 7(6), 381-396.
Roy, K., Hawlader, B., Kenny, S., Moore, I., 2018. Upward pipe–soil interaction for shallowly buried pipelines in dense sand. J. Geotech. Geoenviron. Eng. 144(11), 04018078.
Saberi, M., Annan, C.D., Konrad, J.M., 2018. On the mechanics and modeling of interfaces between granular soils and structural materials. Arch. Civ. Mech. Eng. 18, 1562-1579.
Sadeghirad, A., Brannon, R.M., Burghardt, J., 2011. Converted particle domain interpolation technique to extend applicability of the material point method for problems involving massive deformations. Int. J. Numer. Methods Eng. 86, 1435-1456.
Sadeghirad, A., Brannon, R.M., Guilkey, J., 2013. Second-order convected particle domain interpolation (CPDI2) with enrichment for weak discontinuities at material interfaces. Int. J. Numer. Methods Eng. 95, 928-952.
Saito, H., Korup, O., Uchida, T., Hayashi, S., Oguchi, T., 2014. Rainfall conditions, typhoon frequency, and contemporary landslide erosion in Japan. Geology 42(11), 999-1002.
Scaringi, G., Fan, X., Xu, Q., Liu, C., Ouyang, C., Domènech, G., Yang, F., Dai, L., 2018a. Some considerations on the use of numerical methods to simulate past landslides and possible new failures: the case of the recent Xinmo landslide (Sichuan, China). Landslides 15, 1359-1375.
Scaringi, G., Hu, W., Xu, Q., Huang, R., 2018b. Shear-rate-dependent behavior of clayey bimaterial interfaces at landslide stress levels. Geophys. Res. Lett. 45, 766-777.
Scaringi, G., Loche, M., 2022. A thermo-hydro-mechanical approach to soil slope stability under climate change. Geomorphology 401, 108108.
Shen, L., Chen, Z., 2005. A silent boundary scheme with the material point method for dynamic analyses. Comput Model Eng Sci. 7 (3), 305-320.
Shi, B., Zhang, Y., Zhang, W., 2018. Analysis of the entire failure process of the rotational slide using the material point method. Int. J. Geomech. 18(8), 04018092.
Shi, B., Zhang, Y., Zhang, W., 2019. Run-out of the 2015 Shenzhen landslide using the material point method with the softening model. Bull. Eng. Geol. Environ. 78, 1225-1236.
Shi, J.J., Zhang, W., Wang, B., Li, C.Y., Pan, B., 2020. Simulation of a submarine landslide using the coupled material point method. Math. Probl. Eng. 2020, 1-14.
Sim, W.W., Towhata, I., Yamada, S., 2012. One-g shaking-table experiments on buried pipelines crossing a strike-slip fault. Géotechnique 62(12), 1067-1079.
Soga, K., Alonso, E., Yerro, A., Kumar, K., Bandara, S., 2016. Trends in large-deformation analysis of landslide mass movements with particular emphasis on the material point method. Géotechnique 66(3), 248-273.
Sołowski, W.T., Berzins, M., Coombs, W.M., Guilkey, J.E., Möller, M., Tran, Q.A., Adibaskoro, T., Seyedan, S., Tielen, R., Soga, K., 2021. Material point method: overview and challenges ahead. Adv. Appl. Mech. 54, 113-204.
Steffen, M., Kirby, R.M., Berzins, M., 2008. Analysis and reduction of quadrature errors in the material point method (MPM). Int. J. Numer. Methods Eng. 76(6), 922–948.
Steffffen, M., Wallstedt, P., Guilkey, J., Kirby, R., Berzins, M., 2008. Examination and analysis of implementation choices within the material point method (MPM). Comput. Model. Eng. Sci. 31, 107-127.
Sulsky, D., Chen, Z., Schreyer, H.L., 1994. A particle method for history-dependent materials. Comput. Methods Appl. Mech. Eng. 118(1-2), 179-196.
Talmon, M., Martinelli, M., Luger, D., 2019. Numerical simulation of cutting tests on layered sand and clay. In: Proc. 22nd World Dredging Congress, Shanghai, China.
Tan, D.Y., Yin, J.H., Feng, W.Q., Zhu, Z.H., Qin, J.Q., Chen, W.B., 2019. New simple method for calculating impact force on flexible barrier considering partial muddy debris flow passing through. J. Geotech. Geoenviron. Eng. 145(9), 04019051.
Tan, Y., Lu, Y., 2017. Forensic diagnosis of a leaking accident during excavation. J. Perform. Construct. Facil. 31, 04017061.
Tang, C.S., Zhu, C., Cheng, Q., Zeng, H., Xu, J.J., Tian, B.G., Shi, B., 2021. Desiccation cracking of soils: A review of investigation approaches, underlying mechanisms, and influencing factors. Earth Sci. Rev. 216, 103586.
Tariq, S., Hu, Z., Zayed, T., 2021. Micro-electromechanical systems-based technologies for leak detection and localization in water supply networks: A bibliometric and systematic review. J. Cleaner Prod. 289, 125751.
Tran, Q.A., Grimstad, G., Ghoreishian Amiri, S.A., 2024. MPMICE: A hybrid MPM‐CFD model for simulating coupled problems in porous media. Application to earthquake‐induced submarine landslides. Int. J. Numer. Methods Eng. 125 (5), e7383.
Tran, Q.A., Sołowski, W., 2019. Temporal and null‐space filter for the material point method. Int. J. Numer. Methods Eng. 120(3), 328-360.
Tu, S., Li, W., Zhang, C., Wang, L., Wang, S., Zhao, Y., Wu, J., 2023. Face stability analysis of tunnels in saturated soil considering soil-fluid coupling effect via material point method. Comput. Geotech. 161, 105592.
Uesugi, M., Kishida, H., Tsubakihara, Y., 1988. Behavior of sand particles in sand-steel friction. Soils Found. 28(1), 107-118.
Vermeer, P.A., Yuan, Y., Beuth, L., Bonnier, P., 2009. Application of interface elements with the Material Point Method. In 18th Int. Conf. Soil Mech. Geotech. Eng., Paris, France.
Vicari, H., Tran, Q.A., Nordal, S., Thakur, V., 2022. MPM modelling of debris flow entrainment and interaction with an upstream flexible barrier. Landslides 19(9), 2101-2115.
Wang, B., Vardon, P.J., Hicks, M.A., 2016a. Investigation of retrogressive and progressive slope failure mechanisms using the material point method. Comput. Geotech. 78, 88-98.
Wang, B., Vardon, P.J., Hicks, M.A., 2016b. Preliminary analysis of rainfall-induced slope failures using the material point method. In Proc. 12th Int. Symp. Landslides, Naples, Italy, 2037-2042.
Wang, B., Vardon, P.J., Hicks, M.A., 2018. Rainfall-induced slope collapse with coupled material point method. Eng. Geol. 239, 1-12.
Wang, B., Vardon, P.J., Hicks, M.A., Chen, Z., 2016c. Development of an implicit material point method for geotechnical applications. Comput. Geotech. 71, 159-167.
Wang, D., Wang, B., Jiang, Q., Guo, N., Zhang, W., He, K., 2022a. Large deformation slope failure—A perspective from multiscale modelling. Comput. Geotech. 150, 104886.
Wang, D., Wang, B., Yuan, W., Liu, L., 2023a. Investigation of rainfall intensity on the slope failure process using GPU-accelerated coupled MPM. Comput. Geotech. 163, 105718.
Wang, D., Zhu, H., Zhou, G., Yu, W., Wang, B., Zhou, W., 2024a. Monitoring shear deformation of sliding zone via fiber Bragg grating and particle image velocimetry. J. Rock Mech. Geotech. Eng. 16(1), 231-241.
Wang, D.Y., Zhu, H.H., Wang, B.J., Shi, B., 2021a. Performance evaluation of buried pipe under loading using fiber Bragg grating and particle image velocimetry techniques. Measurement 186, 110086.
Wang, G., You, G., Zhu, J., Yu, J., Gong, X., Wu. J., 2016d. Investigations of Changjing earth fissures, Jiangyin, Jiangsu, China. Environ. Earth Sci. 75 (6), 502.
Wang, J., Lin, S.Q., Tan, D.Y., Yin, J.H., Zhu, H.H., Kuok, S.C., 2024b. A novel method for integrity assessment of soil-nailing works with actively heated fiber-optic sensors. J. Geotech. Geoenviron. Eng. 150(8), 04024063.
Wang, L., Coombs, W.M., Augarde, C.E., Brown, M., Knappett, J., Brennan, A., Richards, D., Blake, A., 2017. Modelling screwpile installation using the MPM. Procedia Eng. 175, 124-132.
Wang, L., Coombs, W.M., Augarde, C.E., Cortis, M., Brown, M.J., Brennan, A.J., Knappett, J.A., Davidson, C., Richards, D., White, D.J., Blake, A.P., 2021b. An efficient and locking‐free material point method for three‐dimensional analysis with simplex elements. Int. J. Numer. Methods Eng. 122(15), 3876-3899.
Wang, S., Zhao, L., Liu, Y., 2023b. A concurrent multiscale method based on smoothed molecular dynamics for large-scale parallel computation at finite temperature. Comput. Methods Appl. Mech. Eng. 406, 115898.
Wang, Y., Gao, D., Fang, J., 2015. Finite element analysis of deepwater conductor bearing capacity to analyze the subsea wellhead stability with consideration of contact interface models between pile and soil. J. Pet. Sci. Eng. 126, 48-54.
Wang, Y., Gao, D., Meng, C., 2022b. Numerical simulation analysis on the lateral dynamic characteristics of deepwater conductor considering the pile-soil contact models. J. Mar. Sci. Eng. 10(10), 1540.
Wang, Y., Shi, J., Ng, C.W.W., 2011. Numerical modeling of tunneling effect on buried pipelines. Can. Geotech. J. 48(7), 1125-1137.
Więckowski, Z., 2004. The material point method in large strain engineering problems. Comput. Methods Appl. Mech. Eng. 193(39-41), 4417-4438.
Wieckowski, Z., 2013. Enhancement of the Material Point Method for fluid-structure interaction and erosion. Delft, Netherlands, Deltares.
Wols, B.A., van Thienen, P., 2014. Modelling the effect of climate change induced soil settling on drinking water distribution pipes. Comput. Geotech. 55, 240-247.
Wu, B., Zhu, H.H., Cao, D.F., Liu, X.F., Liu, T.X., 2023. Fiber optic sensing-based field investigation of thermo-hydraulic behaviors of loess for characterizing land–atmosphere interactions. Eng. Geol. 315, 107019.
Xia, G., Liu, C., Xu, C., Le, T., 2021. Dynamic analysis of the high‐speed and long‐runout landslide movement process based on the Discrete Element Method: A case study of the Shuicheng Landslide in Guizhou, China. Adv. Civ. Eng. 1, 8854194.
Xie, T.C., Zhu, H.H., Tan, D.Y., Shukla, S.K., 2024a. Modeling pipe-soil interaction under surface loading using material point method. Tunn. Undergr. Space Technol. 147, 105709.
Xie, T.C., Zhu, H.H., Zhang, C.X., Liu, W., Tan, D.Y., Zhang, W., 2024b. Modeling pipe–soil interaction under lateral movement using material point method. J. Pipeline Syst. Eng. Pract. 15(1), 04023058.
Xie, T.C., Zhu, H.H., Zhang, C.X., Zhang, W., 2023. Modeling strip footings on slopes using the material point method. Bull. Eng. Geol. Environ. 82(4), 99.
Xie, X.C., Ceccato, F., Zhou, M.L., Zhang, D.M., 2022. Hydro-mechanical behaviour of soils during water-soil gushing in shield tunnels using MPM. Comput. Geotech. 145, 104688.
Yang, Y.S., Qiu, L.C., 2020. MPM simulation of uplift resistance of enlarged base piles in sand. Soils Found. 60(5), 1322-1330.
Ye, X., Zhu, H.H., Cheng, G., Pei, H.F., Shi, B., Schenato, L., Pasuto, A., 2024. Thermo-hydro-poro-mechanical responses of a reservoir-induced landslide tracked by high-resolution fiber optic sensing nerves. J. Rock Mech. Geotech. Eng. 16(3), 1018-1032.
Yerro, A., Alonso, E.E., Pinyol, N.M., 2015. The material point method for unsaturated soils. Géotechnique 65(3), 201-217.
Yerro, A., Alonso, E.E., Pinyol, N.M., 2016. Run-out of landslides in brittle soils. Comput. Geotech. 80, 427-439.
Yerro, A., Girardi, V., Martinelli, M., Ceccato, F., 2022. Modelling unsaturated soils with the Material Point Method. A discussion of the state-of-the-art. Geomech. Energy Environ. 32, 100343.
Yerro, A., Soga, K., Bray, J., 2019. Runout evaluation of Oso landslide with the material point method. Can. Geotech. J. 56(9), 1304-1317.
Yildizdag, M.E., 2023. Numerical modeling and simulation of material extrusion-based 3-D printing processes with a material point method framework. Contin. Mech. Thermodyn. 1-18.
Yimsiri, S., Soga, K., Yoshizaki, K., Dasari, G.R., O’Rourke, T.D., 2004. Lateral and upward soil-pipeline interactions in sand for deep embedment conditions. J. Geotech. Geoenviron. Eng. 130 (8), 830-842.
Ying, C., Zhang, K., Wang, Z.N., Siddiqua, S., Makeen, G.M.H., Wang, L., 2021. Analysis of the run-out processes of the Xinlu Village landslide using the generalized interpolation material point method. Landslides 18, 1519-1529.
York, A.R., Sulsky, D., Schreyer, H.L., 2000. Fluid–membrane interaction based on the material point method. Int. J. Numer. Methods Eng. 48(6), 901-924.
Yost, K., Martinelli, M., Yerro, A., Green, A., de Lange, W., 2023. Addressing complexities in MPM modeling of calibration chamber cone penetrometer tests in homogenous and highly interlayered soils. Comput. Geotech. 158, 105378.
Yost, K.M., Yerro, A., Green, R.A., Martin, E., Cooper, J., 2022. MPM modeling of cone penetrometer testing for multiple thin-layer effects in complex soil stratigraphy. J. Geotech. Geoenviron. Eng. 148(2), 04021189.
Yu, J., Zhao, J., Liang, W., Zhao, S., 2024. Multiscale modeling of coupled thermo-hydro-mechanical behavior in ice-bonded granular media subject to freeze-thaw cycles. Comput. Geotech. 171, 106349.
Yuan, W.H., Wang, B., Zhang, W., Jiang, Q., Feng, X.T., 2019a. Development of an explicit smoothed particle hydrodynamics method for geotechnical applications. Comput. Geotech. 106, 42-51.
Yuan, W.H., Wang, H.C., Zhang, W., Dai, B.B., Liu, K., Wang, Y., 2021. Particle finite element method implementation for large deformation analysis using Abaqus. Acta Geotech. 16, 2449-2462.
Yuan, W.H., Zhang, W., Bai, B., Wang, Y., 2019b. Application of the particle finite element method for large deformation consolidation analysis. Eng. Comput. 36, 3138-3163.
Yuan, W.H., Zheng, H., Zheng, X., Wang, B., Zhang, W., 2023. An improved semi-implicit material point method for simulating large deformation problems in saturated geomaterials. Comput. Geotech. 161, 105614.
Zabala, F., Alonso, E.E., 2011. Progressive failure of Aznalcóllar dam using the material point method. Géotechnique 61(9), 795-808.
Zdravković, L., 1999. Finite element analysis in geotechnical engineering: theory. Thomas Telford.
Zeng, Z., Zhang, H., Zhang, X., Liu, Y., Chen, Z., 2022. An adaptive peridynamics material point method for dynamic fracture problem. Comput. Methods Appl. Mech. Eng. 393, 114786.
Zhan, Z.Q., Zhou, C., Liu, C.Q., Ng, C.W.W., 2023. Modelling hydro-mechanical coupled behaviour of unsaturated soil with two-phase two-point material point method. Comput. Geotech. 155, 105224.
Zhang, C., Zhu, H., Li, H., 2023a. Modeling pipe-soil interaction under vertical downward relative offset using B-spline material point method. J. Rock Mech. Geotech. Eng. 15(6), 1520-1534.
Zhang, C.X., Zhu, H.H., Zhang, W., Li, H.J., Liu, W., 2022a. Modeling uplift failure of pipes buried in sand using material point method. Tunn. Undergr. Space Technol. 119, 104203.
Zhang, D.M., Xie, X.C., Zhou, M.L, Huang, Z.K., Zhang, D.M., 2021. An incident of water and soil gushing in a metro tunnel due to high water pressure in sandy silt. Eng. Fail. Anal. 121, 105196.
Zhang, D.Z., Ma, X., Giguere, P.T., 2011. Material point method enhanced by modified gradient of shape function. J. Comput. Phys. 230(16), 6379-6398.
Zhang, G., Zhang, J., 2009. State of the art: Mechanical behavior of soil–structure interface. Prog. Nat. Sci. 19(10), 1187-1196.
Zhang, H., Yang, J., Wang, L., Xu, Y., Lan, S., Luo, J., Chang, Z., 2023b. Experimental and numerical investigation on failure mechanism of expansive soil subgrade slope. Scientific Reports 13, 19795.
Zhang, H.W., Wang, K.P., Chen, Z., 2009. Material point method for dynamic analysis of saturated porous media under external contact/impact of solid bodies. Comput. Methods Appl. Mech. Eng. 198(17-20), 1456-1472.
Zhang, P., Liu, L.L., Zhang, S.H., Cheng, Y.M., Wang, B., 2022b. Material point method-based two-dimensional cohesive-frictional slope stability analysis charts considering depth coefficient effect. Bull. Eng. Geol. Environ. 81(5), 206.
Zhang, R., Gomaa, S.M., Hussein, M., Zayed, T., Meguid, M., 2023c. Review of numerical approaches used in soil-pipe interaction analysis of water mains. Transp. Geotech. 42, 101008.
Zhang, W., Maeda, K., Saito, H., Li, Z., Huang, Y., 2016a. Numerical analysis on seepage failures of dike due to water level-up and rainfall using a water–soil-coupled smoothed particle hydrodynamics model. Acta Geotech. 11, 1401-1418.
Zhang, X., Chen, Z., Liu, Y., 2016b. The material point method: A continuum-based particle method for extreme loading cases. Academic Press.
Zhao, L., Qiao, N., Huang, D., Zuo, S., Zhang, Z., 2022a. Numerical investigation of the failure mechanisms of soil–rock mixture slopes by material point method. Comput. Geotech. 150, 104898.
Zhao, S., Chen, H., Zhao, J., 2023a. Multiscale modeling of freeze-thaw behavior in granular media. Acta Mech. Sin. 39(1), 722195.
Zhao, S., He, S., Li, X., Deng, Y., Liu, Y., Yan, S., Bai, X., Xie, Y., 2021. The Xinmo rockslide-debris avalanche: An analysis based on the three-dimensional material point method. Eng. Geol. 287, 106109.
Zhao, S., Zhao, J., Liang, W., Niu, F., 2022b. Multiscale modeling of coupled thermo-mechanical behavior of granular media in large deformation and flow. Comput. Geotech. 149, 104855.
Zhao, S., Zhu, L., Liu, W., Li, X., He, S., Scaringi, G., Tang, X., Liu, Y., 2023b. Substratum virtualization in three-dimensional landslide modeling with the material point method. Eng. Geol. 315, 107026.
Zhao, Y., Choo, J., Jiang, Y., Li, L., 2023c. Coupled material point and level set methods for simulating soils interacting with rigid objects with complex geometry. Comput. Geotech. 163, 105708.
Zhao, Y., Choo, J., Jiang, Y., Li, M., Jiang, C., Soga, K., 2022c. A barrier method for frictional contact on embedded interfaces. Comput. Methods Appl. Mech. Eng. 393, 114820.
Zheng, X., Wang, S., Yang, F., Yang, J., 2024. Material point method simulation of hydro-mechanical behaviour in two-phase porous geomaterials: A state-of-the-art review. J. Rock Mech. Geotech. Eng. 16(6), 2341-2350.
Zhou, Z., Yin, Z.Y., He, G.F., Zhang, P., Jiang, M., 2024. The potential of a multi-fidelity residual neural network based optimizer to calibrate DEM parameters of rock-like bonded granular materials. Comput. Geotech. 168, 106137.
Zhu, H.H., 2023. Engineering geological interfaces: from multivariate characterization to evolution mechanism. Bull. Geol. Sci. Technol. 42(1), 1-20 (in Chinese).
Zhu, H.H., Xie, T.C., Zhang, W., Shukla, S.K., 2023. Numerical simulations of a strip footing on the soil slope with a buried pipe using the material point method. Int. J. Geomech. 23(11), 04023190.
Zhu, H.H., Yin, J.H., Yeung, A.T., Jin, W., 2011, Field pullout testing and performance evaluation of GFRP soil nails. J. Geotech. Geoenviron. Eng. 137(7), 633-642.
Zhu, Y., Ishikawa, T., Zhang, Y., Nguyen, B.T., Subramanian, S.S., 2022. A FEM-MPM hybrid coupled framework based on local shear strength method for simulating rainfall/runoff-induced landslide runout. Landslides 19(8), 2021-2032.
Zwanenburg, W., Wittekoek, R., Martinelli, M., Alderlieste, E., 2023. The effect of finite layer thickness; a validation of MPM analysis by centrifuge testing. In: Proc. 10th European Conf. on Numerical Methods in Geotechnical Engineering 1-6.
