Material point method simulations of sand deformation and failure around tunnel controlled by support pressure
张春新, 朱鸿鹄*, 李豪杰, 张巍, 刘春(南京大学 地球科学与工程学院,江苏 南京 210023)
ZHANG Chun-xin, ZHU Hong-hu*, LI Hao-jie, ZHANG Wei, LIU Chun (School of Earth Sciences and Engineering, Nanjing University, Nanjing 210023, China)
摘要:为了探究隧道周围砂土地层在支护压力减小过程中的变形破坏机理,利用能够进行岩土大变形分析的物质点法(MPM)对该过程进行数值模拟. 研究隧道周围土体的剪切带特征、土拱效应、MPM地面沉降槽形态以及支护压力与地层位移间的关系;验证该数值方法研究隧道诱发变形的可靠性. 对比预测结果与已有试验和理论表明,MPM能够准确预测出隧道支护压力降低引起的地层变形和极限支护压力,并且可以得到地层整体失稳及坍塌后的变形行为. 在此基础上,分析隧道埋深比和砂土内摩擦角对变形过程中土拱效应强弱、极限支护压力和地层变形的影响.
关键词: 隧道施工 ; 物质点法(MPM) ; 土拱效应 ; 极限支护压力 ; 沉降槽
Abstract: To explore the deformation and failure mechanism of sand foundation induced by the decrease of tunnel support pressure, the material point method (MPM), a large deformation analyzing method in geotechnical engineering was used to simulate the whole process. The characteristics of localized shear bands, the arching effect, the settlement trough shape, and the relationship between support pressure and ground movement were investigated. The reliability of MPM in analyzing tunnel-induced soil deformation was verified. By comparing the simulated results with experimental and theoretical data, it is shown that MPM can accurately predict the ground deformation caused by the reduction of tunnel support pressure and the ultimate support pressure, and obtain the overall deformation behavior before and after tunnel collapse. On this basis, the influence of cover depth-to-diameter ratios and friction angles on the arching effect, the limiting support pressure and the strata deformation were investigated.
Keywords: tunnel construction; material point method (MPM); soil arching effect; ultimate support pressure; settlement trough
随着地下空间开发和城市轨道交通的迅速发展,盾构施工过程中遭遇的工程地质条件和掘进环境越来越复杂,在施工中必须充分保证岩土体的自稳性. 但是在工程实践中,隧道施工诱发的周围地层沉降变形,常常致使附近建筑物和管线等设施出现过大变形或局部破坏[1-3]. 当开挖面支护不当或支护压力过小时,容易造成严重的失稳事故[4-5].
国内外众多学者围绕隧道开挖面稳定性及支护压力对地面沉降的影响开展了较为系统的研究. Mair等[6]通过一系列离心模型试验,研究了饱和软土中盾构开挖面的稳定性问题. 陈仁朋等[7]基于模型试验,探究干砂中隧道埋深比对开挖面极限支护力及地表沉降的影响,并将失稳全过程分为弹塑性、局部失稳和整体失稳3个阶段. 米博等[8]研究了在不同水头条件下,开挖渗流对开挖面支护压力和地层失稳模式的影响. 朱伟等[9-10]采用有限差分法分别对砂土、黏土中盾构开挖面的变形与破坏进行数值模拟研究.
除了隧道开挖面以外,隧道变形或隧洞支护反力变化对地基变形影响的研究主要分为2类:1)一定地层损失下周围土体的变形特性,如Marshall等[11-12]基于隧道离心试验,分析不同深度和不同体积损失下砂土中沉降槽的特征,并进行离散元模拟;Song等[13]分别采用有限元和离散元模拟隧道在一定体积损失下引起的土体变形,并与应力控制、位移控制2种隧道边界的离心试验结果进行对比. 2)隧道支护压力对地层位移的影响,如周小文等[14]通过离心模型试验研究砂土中隧洞开挖支护反力与地面沉降的关系. 以上这些模型试验和数值模拟研究多侧重于地层损失或支护反力变化下周围土体的沉降研究,对于地层变形破坏的研究相对较少.
数值模拟为评估隧道及周边土体的力学性质、探究土体变形机理提供了有效手段. 但是有限元法处理大变形问题时往往发生严重的网格畸变,难以有效模拟隧道周围的大变形[15]. 离散元法可以模拟隧道变形引起的地面沉降槽形状及土体应力的变化,但很难精确建立隧道支护压力和地面沉降的关系曲线[12, 16]. 近些年发展起来的物质点法(material point method,MPM)[17-19]是介于粒子法与有限元法之间的数值方法,非常适合大变形模拟. 该方法将连续体离散为一系列(物)质点,质点携带所有物质和运动信息,背景网格覆盖整个求解域,通过插值函数将所需变量从质点映射到背景网格节点以求解动量方程,而后将求解的运动信息从背景网格节点映射回质点以更新质点信息. 在此过程中,计算网格不携带任何信息,仅用于求解平衡方程. 物质点法基于连续介质动量方程及其弱形式,本构模型和参数更容易根据试验或实际工况确定,在模拟滑坡[20-22]、强夯[23]、沉桩[24]、隧道变形引发的如地层失稳[25]的岩土大变形问题方面具有明显优势.
本文采用MPM模拟砂土中隧道支护压力降低引起地面变形的过程,研究周边土体的变形、剪切带的发育、土拱效应的强弱、地面沉降槽形态等,并定量分析隧道埋深及土体强度对土拱效应、极限支护压力和周围土体变形模式的影响.
1. 物质点法数值模型
1.1. 模型建立
本文采用剑桥大学、加州大学伯克利分校等联合开发的动态显式MPM程序Anura3D[19],建立如图1所示的隧道二维平面应变模型. 图中,C为土体覆盖层厚度,D为隧道直径. 模型尺寸根据Marshall的离心试验原型[11]确定. 由于显示计算中临界时间步长遵循CFL(Courant-Friedrichs-Lewy)条件,因此原型尺寸下,可获得更大的时间步长和更高的计算效率. Fern等[25-26]在模拟离心模型试验时均采用原型建模.
在隧道周围设置一层弹性薄膜,将支护压力施加于薄膜内侧,通过薄膜将支护荷载分散到周围土体的物质点上,防止因某个物质点应力集中而发生振荡. 薄膜与土体接触间不设置接触条件. 模型的边界与离心机刚性箱边界保持一致,底部和两侧均施加对称边界条件。如图1所示,计算区域采用规则的三角形单元进行离散,每个激活单元内设置3个物质点. 通过初步模拟,确定单元长度为0.6 m,并将隧道周围区域的网格加密.
为了得到更加精确的应力计算和平滑的应力分布,模拟中采用物质点−高斯点混合积分法[27]和体应变平滑算法[19]. 将局部阻尼系数设置为0.10以减少因支护压力降低而引起的应力振荡.
1.2. 模型参数
结合离心机试验的原型尺寸[11]及实际工况,选取隧道直径D为6 m,隧道埋深C分别为9、15、21 m,对应埋深比C/D分别为1.5、2.5、3.5.
在Marshall等[11]开展的离心试验中,干砂的最大、最小孔隙比分别为0.97、0.64,相对密度为0.9,比重为2.67,可得砂土初始孔隙比e=0.673,重度γ=15.96 kN/m3,但文献[11]中并未提及土体的强度参数. 本文土体本构模型采用Mohr-Coulomb模型,取弹性模量E=25 MPa,泊松比v=0.33,为了研究砂土强度对土体变形的影响,取内摩擦角φ分别为15°、25°、35°. 弹性薄膜采用线弹性模型,为了避免临界时间步长过小,将薄膜设置为厚度l=20 cm的实体单元. 薄膜刚度取为土体刚度的1/10,弹性模量Ef=2.5 MPa,泊松比vf=0.4. 静止土压力系数K0=0.5.
1.3. 计算过程
本文重点讨论在不同工况下支护压力变化对周围土体变形的影响,因此数值计算不考虑开挖过程和支护结构,直接将隧道支护压力施加在弹性膜上,且初始压力等于隧道中心的原位地应力[9–10, 25]:
σT0=γ(C+D/2). (1)
式中: σ0TσT0为隧道的初始支护压力.
λ=1−σT/σ0T. (2)
2. 数值模拟结果及分析
2.1. 支护压力−地面沉降曲线
支护压力−地面沉降关系曲线可反映土体变形及土拱效应随隧道支护压力逐渐下降的变化特征[14]. 当C/D=1.5,φ=25°时,隧道拱顶和地表中心点处物质点MP 59、MP 4938的荷载−位移曲线如图2所示. 根据模拟结果,可将土体变形过程划分为3个阶段:1)土体沉降较小且缓慢发展. 当σT降低到64 kPa(λ=0.67)时,拱顶沉降 ΔZV和地表中心点处沉降 ΔZS分别为4.9、3.3 cm. 在此之前,拱顶和地面中心点处变形均较小,土体抗剪强度逐渐发挥,且基本处于弹性变形阶段. 2)土体变形迅速发展. 地层变形在后两级支护压力(σT分别为57、51 kPa)下迅速发育,拱顶竖向位移分别为13、32 cm,地面中心点沉降分别达到10、26 cm. 此阶段沉降增长速率迅速增加,曲线斜率增大,土体局部失稳并发生大变形. 3)土体整体失稳. 支护压力降低到45 kPa(λ=0.77)时,隧道完全坍塌且被土填充. 整体失稳后,随着隧道支护压力降低及周围土体压实作用,土体发生很小的沉降.
整个过程的地面沉降曲线呈S形,隧道的极限支护压力等于整体坍塌前的支护压力值,为51 kPa(λ=0.73). 对比文献[14]砂土中隧洞埋深比C/D=2的离心试验[14](见图2),模拟所得的拱顶、地表的沉降及沉降发育过程,均与试验结果相近,但由于埋深比不同,试验所得的极限支护压力略低.
2.2. 土体变形及剪切带发育特征
该工况中隧道坍塌前后两级支护压力下的土体位移u如图3所示. 在隧道极限支护压力(σT=51 kPa)下,拱顶上部土体呈明显的烟囱状位移,与离心模型试验得到的土体位移模式[11, 14]一致. 当支护压力σT降为45 kPa时,周围地层坍塌,除了弹性膜占据一定空间,隧道基本被周围土体填充,且土体变形范围在地表处明显变宽. 此时,地表变形区延伸到 ±12 m的位置,即 ±2D范围. 土体位移主要发生在隧道上方,由于卸载效应,隧道下方也出现了少量变形.
为了进一步探究隧道周围土体的变形机理,取隧道坍塌前两级支护压力下的偏应变 εd(广义剪应变)云图,如图4所示. 与不排水黏土中隧道坍塌时出现的心型偏应变区[20]不同,砂土中偏应变从拱顶两侧呈一定宽度垂直发展至地表,沿竖向基本对称分布,Bym等[16]的离散元模拟也得到同样的结论. 在模拟中出现了偏应变轻微的不对称分布,这是由于网格剖分和弹性膜变形不完全对称造成的. 在极限支护压力(σT=51 kPa)作用下,土体的剪切带(偏应变发育区)变宽并扩展到地表,剪切带内、外两侧土体沉降不均匀,内侧土体呈现明显的烟囱状位移,外侧土体位移较小,土体沿剪切带发生破坏. 当偏应变未延伸到土体表层时,浅层土体变形较小,基本处于弹性状态.
Marshall等[11]对比研究不同深度沉降槽的形状变化,推断浅埋隧道拱顶上部土体由于剪应变较高而发生剪缩,拱顶两侧因剪应变稍低存在剪胀效应. 与图4(b)对应的土体体应变 εv如图5所示. 由图4(b)和图5可知,土体中剪切带位于拱顶两侧,而非隧道顶部区域. 隧道两侧土体出现明显体缩,但该区域位于剪切带(图5中深色框线)之外,可能是拱效应使得剪切带内侧土体自重以附加压应力形式分散到两侧土体. 此外,隧道底部土体由于卸载,出现明显的回弹.
剪切带内两物质点的偏应力q和平均应力p随支护压力的变化如图6所示. 由图1可见,物质点MP 2161(x=6 m,z=9 m)、MP 8084(x=6 m,z=3 m)距隧道中心线的水平距离均为D,距地表竖向距离分别为0.5D、1.5D. 随着隧道支护压力的降低(σT>64 kPa),拱顶附近质点MP 8084偏应力逐渐增加并达到抗剪强度,地表附近MP 2161的偏应力和平均应力(压缩为负)均变化不大,此时地表土体变形较小,处于弹性状态. 当σT=57 kPa(λ=0.70)时,拱顶附近土体发生塑性变形,偏应力减小,土体局部失稳,随后剪切带扩展到地表,地表土体的偏应力迅速增大,平均应力减小. 随着支护压力进一步降低,周围地层整体失稳,当σT=45 kPa(λ=0.77)时隧道完全坍塌且被土体填充,之后,土体处于残余应力状态且应力基本保持不变. 但在坍塌后到支护压力降为0的过程中,隧道周围土体仍然有小部分变形发生,因此偏应力略有增加.
在隧道周围土体大变形过程中,拱顶附近的土体受到隧道变形影响,首先进行应力调整,逐渐发挥抗剪强度,出现剪切带并向地表扩展,而后,地表土体偏应力增大,剪切带贯通,隧道坍塌. 显然,在隧道发生大变形之前,拱顶两侧土体中早已产生较大剪切变形,此处土体变形可作为隧道坍塌预报的重要监测信息.
2.3. 土拱效应
该工况下隧道拱顶以上0.5D土层的归一化竖向应力 σv/σ0v、归一化水平应力 σh/σ0h、剪应力τxy分布如图7所示. 随着隧道及周围土体的变形,地层内拱效应逐渐加强,土拱内竖向应力σv减小,水平应力σh增加,隧道上方地层受剪切带两侧土体挤压,上方土体自重通过剪应力传递到两侧土体. 图7中剪应力值较大处即剪切带位置,可见随支护压力减小,剪切带外移加宽,剪应力逐渐增大,直到σT=57 kPa(λ=0.70),已接近隧道的极限支护压力,剪切带始终在 ±D范围内. 拱外土体σv增大,最大值在剪切带之外;拱外σh减小,在剪切带附近变化较小. 距隧道中心 ±2D范围外,土体应力变化不大. 汪大海等[28]通过有限元对砂土中浅埋隧道极限状态时地层中拱效应进行研究,得到类似规律.
2.4. 地表沉降槽特征
隧道支护压力σT在102~51 kPa(λ=0.47~0.73)范围内(对应隧道坍塌前的9级支护压力),每一级支护压力下的地面沉降值及拟合曲线如图8所示. 基于最小二乘法,采用Peck公式[29]对数值模拟的沉降进行拟合,得到的沉降槽宽度系数K在0.45~0.7之间,较砂土中的典型K值(0.25~0.45)[9]偏大. 由图8(a)可知,当支护压力较高、土体变形较小时(σT>96 kPa,λ<0.50),模拟的沉降值与拟合的高斯曲线一致性较好;随着土体变形增大(σT<96 kPa,λ>0.50),尤其发生局部失稳后,沉降值在x>1.5D范围内模拟值与拟合曲线存在偏差. 可见,相较于模拟结果,Peck公式给出的沉降槽较窄,且在隧道支护压力较低的情况下,在x>1.5D范围内沉降仍然不会显著增加. 这可能是数值结果中模拟的剪切带过厚[25]或者实际工况下土体的非均质性和各向异性造成的,但观察到周小文等[14]的离心试验结果,在距隧道中心1.5D之外地表仍有较大沉降值,可见Peck公式在描述砂土中沉降时,可能存在精度不足的问题. 因此,采用Vorster等[3]提出的修正高斯曲线对沉降值进行拟合:
ΔZ=nΔZmax(n−1)+exp[α(x2/i2)], (3)
n=exp(α)2α−12α+1+1. (4)
式中: ΔZ为沉降值, ΔZmax为最大沉降值,x为距隧道中心线的距离, ΔZmax、i、α、n均为拟合参数. 结果表明,数值模拟结果的拟合优度较好,相关系数R2均在0.998到0.999之间. 由图8可以看出,相较于Peck公式,修正高斯曲线与模拟值的更吻合,可以更好地描述砂土中的沉降,这与Marshall等[11]的离心试验沉降数据的拟合特征相同.
3. 隧道变形与破坏影响因素分析
隧道埋深、地层条件等因素都会对隧道开挖、支护过程中土体的变形和破坏产生一定影响,基于此,对隧道条件及土层参数进行相关敏感性分析.
3.1. 隧道埋深比的影响
在隧道直径D=6 m、土体内摩擦角 ϕ=25°情况下,研究覆土厚度C分别为9、15、21 m时支护压力减小引起上覆土体变形和剪切带发育的特征.
不同埋深比下,压力折减系数λ与地面中心点处沉降Δz关系如图9所示,根据沉降曲线得到的极限支护压力σTL如表1所示. 随着隧道埋深比增大,极限支护压力所对应的折减系数升高,隧道完全破坏时地表的沉降减小,但相较于上覆土压力的增大量,极限支护压力仅略有增加,这与朱伟等[9]对隧道开挖面极限支护压力的模拟结果一致. 原因是随埋深比增大,土中拱效应发挥,使得土体自稳能力增强. 与本文不同的是,Alagha等[30]在模拟中指出,对于 ϕ>25°的砂土,隧道变形过程中土拱效应可充分发挥,开挖面的极限支护压力比保持在0.17( λ=0.83),基本不受埋深比影响. 这很可能是相对于开挖面的变形,隧道沿径向变形时,土体自稳所需的拱效应更强,此时仍受埋深比控制.
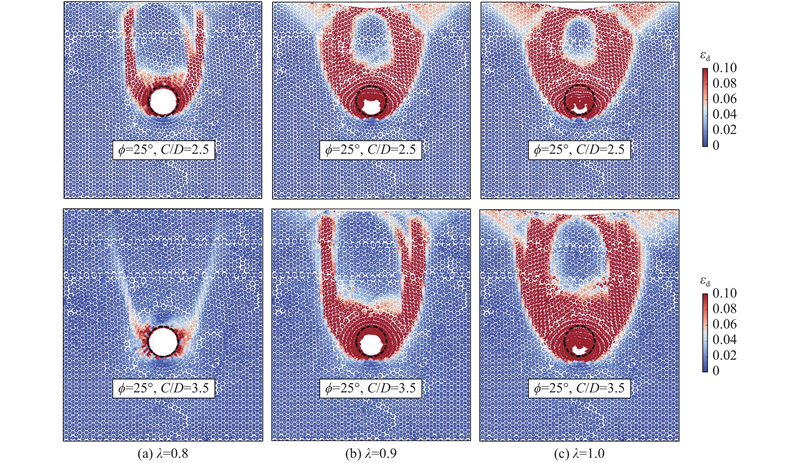
如图10所示为不同压力折减系数下土体的偏应变分布. 由图可知,在极限支护压力附近,土体中剪切带(滑移面)自隧道侧部倾斜发展至顶部,并在隧道上方垂直贯通至地表. 随着支护压力降低,剪切带范围逐渐加宽,拱顶附近土体变形增大,由于滑移面内部土体沉降明显,带动地表附近滑移面外侧土体再次发生主动破坏,并呈现倒三角形的塑性区. 此外,滑移面两侧土体产生塑性变形,隧道上方刚性区逐渐减小;且埋深比越大,地表土体塑性变形越小,刚性区范围越大. 当隧道支护压力降为0时,弹性薄膜和拱效应的作用使得周围土体并未完全坍塌.
3.2. 砂土内摩擦角的影响
砂土材料性质对土体变形破坏的影响主要体现在内摩擦角上. 模拟中保持隧道直径D=6 m、覆土厚度C=15 m,取内摩擦角φ分别为15°、25°、35°进行数值计算,得到不同内摩擦角砂土中压力折减系数λ与地面中心点竖向位移的关系如图11所示,不同内摩擦角下极限支护压力如表2所示. 由图11可见,极限支护压力和对应的折减系数都对砂土的内摩擦角很敏感,内摩擦角越高,极限支护压力越低. 隧道达到极限支护压力前,地表沉降较小,在 ϕ=35°的砂土中,直至支护压力降为0,隧道才完全坍塌,可见此情况下土体中拱效应较强,且在支护压力减小过程中,拱效应逐渐发挥,调整应力分布,保持土体稳定性.
为了直观地了解砂土强度对土拱效应的影响,在拱顶竖向位移为24 cm时,取隧道中心线处地表以下深度H范围内的竖向应力σv作图,如图12所示. 由图可知,在隧道变形过程中,由于拱效应发挥作用,竖向应力沿深度重新分布. 在强度稍弱的土中,内摩擦角较小,土体抵抗相对向下运动的剪切阻力很低,导致竖向应力降低相对较小. 随着土体强度的增加,竖向应力降幅更大,拱效应更加明显,这与文献[30]的模拟结果相符. 由于初始构型中所选取物质点的移动和局部大变形产生的应力振荡,在深度相对较小时,竖向应力相对土体自重应力γH产生较小偏差. 在内摩擦角为15°和35°的砂土中,距地表14m处竖向应力差值可达107 kPa,可见拱效应是确定砂土中隧道支护反力、评价隧道稳定性的重要因素,不同强度砂土中拱效应的强弱差异影响着支护压力值的大小.
如图13所示为不同内摩擦角条件下土体的偏应变云图. 由图可知,在λ=0.95时,强度较低(φ=15°、25°)土体的剪切带已贯通地表,滑移面内部土体沉降已引起两侧土体较大的塑性变形. 对于强度较高(φ=35°)的土体,其拱效应较强,剪切带的抗剪强度分散了滑移面内侧的土体重力,避免了滑移面内部土体的较大沉降和地表的塑性破坏.
4. 结 论
(1)将数值计算结果与已有试验和模拟进行对比,表明物质点法能够准确预测出隧道支护压力降低引起的地层变形和破坏,且可以得到地层整体失稳后的变形行为.
(2)随着隧道变形,砂土中剪切带(滑移面)自隧道侧部倾斜发展至顶部,并在隧道上方垂直贯通至地表,由于滑移面内部土体沉降明显,带动滑移面外侧土体再次发生主动破坏,并在地表附近呈现倒三角形的塑性区.
(3)在支护压力逐级降低的情况下,土体中应力重新分布,土拱效应逐渐增强,使得地层土不会突然发生整体失稳. 在土体变形较大的情况下,修正高斯曲线对地表沉降的拟合效果强于Peck公式.
(4)隧道埋深比、土体内摩擦角不仅会影响极限支护压力,还会对砂土中拱效应的强弱和周围土体的变形破坏模式有重要的影响.
(5)模拟中暂未考虑土体开挖、施工方法或工艺对地面变形的影响,后续将就此做进一步探究.
参考文献(References):
[1] 施成华, 彭立敏, 刘宝琛. 浅埋隧道开挖对地表建筑物的影响[J]. 岩石力学与工程学报, 2004, 23(19): 3310-3316.
SHI Cheng-hua, PENG Li-min, LIU Bao-chen. Influence of shallow tunnel excavation on ground surface buildings[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(19): 3310-3316.
[2] 丁智, 张霄, 周联英, 等. 近距离桥桩与地铁隧道相互影响研究及展望[J]. 浙江大学学报: 工学版, 2018, 52(10): 1943-1953.
DING Zhi, ZHANG Xiao, ZHOU Lian-ying, et al. Research and prospect of interaction between close bridge pile and metro tunnel[J]. Journal of Zhejiang University: Engineering Science, 2018, 52(10): 1943-1953.
[3] VORSTER T E, KLAR A, SOGA K, et al. Estimating the effects of tunneling on existing pipelines[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2005, 131(11): 1399-1410.
[4] ALIABADIAN Z, SHARAFISAFA M, NAZEMI M, et al. Numerical analyses of tunnel collapse and slope stability assessment under different filling material loadings: a case study[J]. Arabian Journal of Geosciences, 2015, 8(3): 1229-1242.
[5] HENCHER S R. The Glendoe tunnel collapse in Scotland[J]. Rock Mechanics and Rock Engineering, 2019, 52: 4033- 4055.
[6] MAIR R J, TAYLOR R N. Theme lecture: bored tunnelling in the urban environment[C]// 14th International Conference on Soil Mechanics and Foundation Engineering. Hamburg: ISSMGE, 1997, 4: 2353-2385.
[7] 陈仁朋,李君,陈云敏,等. 干砂盾构开挖面稳定性模型试验研究[J]. 岩土工程学报, 2011, 33(1): 117-122.
CHEN Ren-peng, LI Jun, CHEN Yun-min, et al. Large-scale tests on face stability of shield tunnelling in dry cohesionless soil[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 33(1): 117-122.
[8] 米博,项彦勇. 砂土地层浅埋盾构隧道开挖渗流稳定性的模型试验和计算研究[J]. 岩土力学, 2020, 41(3): 837-848.
MI Bo, XIANG Yan-yong. Model experiment and calculation analysis of excavation-seepage stability for shallow shield tunneling in sandy ground[J]. Rock and Soil Mechanics, 2020, 41(3): 837-848.
[9] 朱伟, 秦建设, 卢廷浩. 砂土中盾构开挖面变形与破坏数值模拟研究[J]. 岩土工程学报, 2005, 27(8):897-902.
ZHU Wei, QIN Jian-she, LU Ting-hao. Numerical study on face movement and collapse around shield tunnels in sand[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 27(8): 897-902.
[10] 秦建设,虞兴福,钟小春,等. 黏土中盾构开挖面变形与破坏数值模拟研究[J]. 岩土力学, 2007, 28(S1): 511-515.
QIN Jian-she, YU Xing-fu, ZHONG Xiao-chun, et al. Numerical research on face movement and collapse of shield tunneling in silt grounds[J]. Rock and Soil Mechanics, 2007, 28(S1): 511-515.
[11] MARSHALL A M, FARRELL R, KLAR A, et al. Tunnels in sands: the effect of size, depth and volume loss on greenfield displacements[J]. Geotechnique, 2012, 62(5): 385-399.
[12] MARSHALL A M, ELKAYAM I, KLAR A. Ground behaviour above tunnels in sand-DEM simulations versus centrifuge test results[C]// 2009 2nd International Conference on Computational Methods in Tunnelling. Bochum: [s. n.], 2009: 183-190.
[13] SONG G, FRANZA A, ELKAYAM I, et al. A study of greenfield tunnelling in sands using FEM, DEM, and centrifuge modelling[C]// Micro to Macro Mathematical Modelling in Soil Mechanics. Reggio Calabria: [s. n.], 2018: 337-345.
[14] 周小文,濮家骝. 砂土中隧洞开挖引起的地面沉降试验研究[J]. 岩土力学, 2002, 23(5): 559-563.
ZHOU Xiao-wen, PU Jia-liu. Centrifuge model test on ground settlement induced by tunneling in sandy soil[J]. Rock and Soil Mechanics, 2002, 23(5): 559-563.
[15] WONGSAROJ J, SOGA K, MAIR R J. Tunnelling-induced consolidation settlements in London Clay[J]. Geotechnique, 2013, 63(13): 1103-1115.
[16] BYM T, MARKETOS G, BURLAND J B, et al. Use of a two-dimensional discrete-element line-sink model to gain insight into tunnelling-induced deformations[J]. Geotechnique, 2013, 63(9):791-795.
[17] SULSKY D, CHEN Z, SCHREYER H L. A particle method for history-dependent materials[J]. Computer Methods in Applied Mechanics and Engineering, 1994, 118(1): 179–196.
[18] SULSKY D, ZHOU S J, SCHREYER H L. Application of a particle-in-cell method to solid mechanics[J]. Computer Physics Communications, 1995, 87(1-2): 236–252.
[19] FERN J, ROHE A, SOGA K, et al. The Material Point Method for Geotechnical Engineering: A Practical Guide[M]. Boca Raton: CRC Press, 2019.
[20] 史卜涛, 张云, 张巍. 边坡稳定性分析的物质点强度折减法[J]. 岩土工程学报, 2015, 38(9): 1678–1684. SHI Bo-tao, ZHANG Yun, ZHANG Wei. Strength reduction material point method for slope stability[J]. Chinese Journal of Geotechnical Engineering, 2015, 38(9): 1678–1648.
[21] 王斌, 冯夏庭, 潘鹏志, 等. 物质点法在边坡稳定性评价中的应用研究[J]. 岩石力学与工程学报, 2017, 36(9):2146-2155.
WANG Bin, FENG Xia-ting, PAN Peng-zhi, et al. Slope failure analysis using the material point method[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(9): 2146-2155.
[22] 王双, 李小春, 石露, 等. 物质点强度折减法及其在边坡中的应用[J]. 岩土力学, 2016, 37(9):2672-2678. WANG Shuang, LI Xiao-chun, SHI Lu, et al. Material point strength reduction method and its application to slope engineering[J]. Rock and Soil Mechanics, 2016, 37(9): 2672-2678.
[23] 张芮瑜, 孙玉进, 宋二祥. 强夯的物质点法模拟及其能量转化规律分析[J]. 岩土工程学报, 2019, 41(7): 1206–1216.
ZHANG Rui-yu, SUN Yu-jin, SONG Er-xiang. Simulation of dynamic compaction using material point method and analysis of its energy conversion law[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(7): 1206–1216.
[24] PHUONG N T V, VAN TOL A F, ELKADI A S K, et al. Numerical investigation of pile installation effects in sand using material point method[J]. Computers and Geotechnics, 2016, 73:58-71.
[25] FERN J. Modelling tunnel-induced deformations with the material point method[J]. Computers and Geotechnics, 2019, 111: 202–208.
[26] FERN J, DE LANGE D, ZWANENBURG C, et al. Experimental and numerical investigations of dyke failures involving soft materials[J]. Engineering Geology, 2017, 219: 130-139.
[27] BEUTH L, WIECKOWSKI Z, VERMEER P A. Solution of quasi-static large-strain problems by the material point method[J]. International Journal for Numerical & Analytical Methods in Geomechanics, 2011, 35(13): 1451-1465.
[28] 汪大海,贺少辉,刘夏冰,等. 基于主应力旋转特征的浅埋隧道上覆土压力计算及不完全拱效应分析[J]. 岩石力学与工程学报, 2019, 38(6): 1284-1296.
WANG Da-hai, HE Shao-hui, LIU Xia-bing, et al. A modified method for determining the overburden pressure above shallow tunnels considering the distribution of the principal stress rotation and the partially mobilized arching effect[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(6): 1284-1296.
[29] PECK R B. Deep Excavations and tunneling in soft ground[C]// 7th International Conference on Soil Mechanics and Foundation Engineering. Mexico: ISSMGE, 1969: 225-290.
[30] ALAGHA A S N, CHAPMAN D N. Numerical modelling of tunnel face stability in homogeneous and layered soft ground[J]. Tunnelling and Underground Space Technology, 2019, 94, 103096.
引用格式:张春新, 朱鸿鹄, 李豪杰, 张巍, 刘春. 支护压力控制下隧道周围砂土变形破坏物质点法模拟. 浙江大学学报(工学版)[J], 2021, 55(7): 1317-1326 doi:10.3785/j.issn.1008-973X.2021.07.011 (ZHANG Chun-xin, ZHU Hong-hu, LI Hao-jie, ZHANG Wei, LIU Chun. Material point method simulations of sand deformation and failure around tunnel controlled by support pressure. Journal of Zhejiang University(Engineering Science)[J], 2021, 55(7): 1317-1326 doi:10.3785/j.issn.1008-973X.2021.07.011)